Strojové učení nabízí širokou škálu algoritmů, které se liší svým principem i oblastmi využití. Pro začátečníka může být obtížné zorientovat se, který algoritmus zvolit pro konkrétní úlohu. V tomto článku proto srozumitelně představím běžné algoritmy strojového učení, jejich praktické využití a vzájemné porovnání. Probereme klasické metody jako logistická a lineární Regrese, rozhodovací strom, metoda k nejbližším sousedům (KNN), Support Vector Machines (SVM), naivní Bayesův klasifikátor, umělé neuronové sítě (ANN), ale i metody učení bez učitele jako shlukování k-means či analýza hlavních komponent (PCA). Rozšíříme také seznam o pokročilé ensemble metody včetně náhodného lesa (Random Forest) a boosting algoritmů jako AdaBoost, Gradient Boosting (např. implementace XGBoost nebo LightGBM).
Ensemble metody – síla kombinace
Mezi pokročilé přístupy patří ensemble metody, které kombinují více jednoduchých modelů (slabých učitelů) do silnějšího celku. Základní myšlenka spočívá v tom, že chyby jednotlivých modelů se navzájem kompenzují, což vede k lepší generalizaci.
Rozlišujeme tři hlavní přístupy: bagging (Bootstrap Aggregating) trénuje více modelů nezávisle na různých podmnožinách dat a výsledky zprůměruje, čímž snižuje variance modelu. Boosting trénuje modely sekvenčně, každý nový se soustředí na chyby předchozích, a snižuje jak bias, tak variance. Stacking používá metamodel, který se učí kombinovat predikce různých algoritmů – základní modely poskytují predikce, které slouží jako vstupy pro finální metamodel. Stacking je obzvlášť výhodný v soutěžích (Kaggle) a při kombinaci heterogenních base-modelů (např. neuronové sítě + XGBoost + SVM), kde různé algoritmy zachycují odlišné aspekty dat. V následujících sekcích se podíváme na jak na jednotlivé algoritmy jak na konkrétní implementace těchto ensemble přístupů.
Článek vysvětlí, k čemu se jednotlivé algoritmy hodí – například které se používají pro klasifikaci e-mailů (spam filtr), predikci cen nebo rozpoznávání obrázků. Dále porovnáme algoritmy z hlediska přesnosti, výpočetní náročnosti (při trénování vs. při nasazení), interpretovatelnosti modelu a vhodnosti pro malé vs. velké datasety.
Proč mluvíme ve kontextu AI právě o strojovém učení?
Umělá inteligence zahrnuje mnoho přístupů k řešení složitých problémů. Tradiční symbolická AI se spoléhala na expertní systémy s ručně naprogramovanými pravidly, což fungovalo pro úzké domény, ale bylo křehké a neškalovatelné. Automatické plánování a heuristické vyhledávání (známé např. ze šachových programů) vyžadovaly detailní znalost problému.
Strojové učení vnáší zásadní změnu – místo ručního programování pravidel se model učí ze vzorů v datech. To přináší výhody jako škálovatelnost (více dat obvykle znamená lepší model), adaptivitu (model lze doškolovat na nová data) a schopnost generalizace na fuzzy či šumem zasažené případy. Proto dnes ML dominuje počítačovému vidění, zpracování přirozeného jazyka i doporučovacím systémům.
Algoritmy strojového učení a jejich praktické využití
Než se pustíme do detailů, je dobré si uvědomit, že existují různé typy úloh strojového učení. Klasifikace a Regrese jsou úlohy učení s učitelem (supervised learning), kde model predikuje známý výstup (např. kategorii nebo číselnou hodnotu) na základě trénovacích dat.
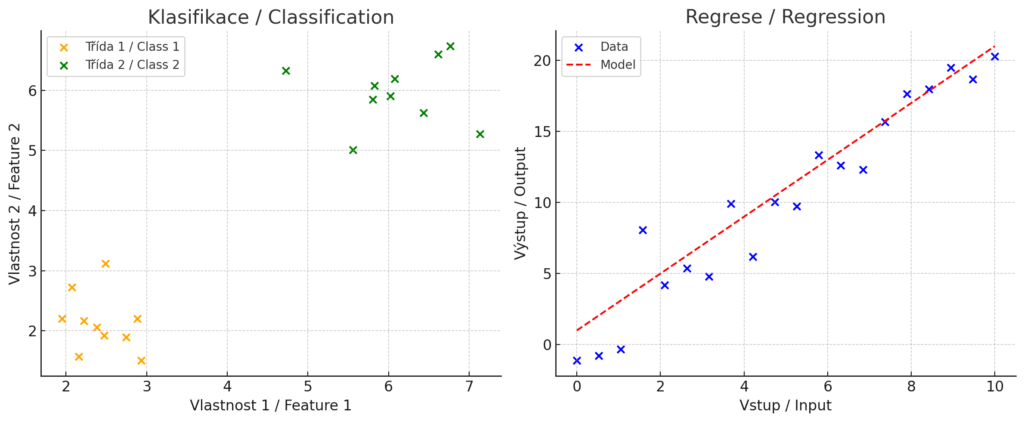
Naproti tomu shlukování a snížení dimenzionality jsou úlohy učení bez učitele (unsupervised learning), kde algoritmus objevuje strukturu v datech bez předem daných správných odpovědí.
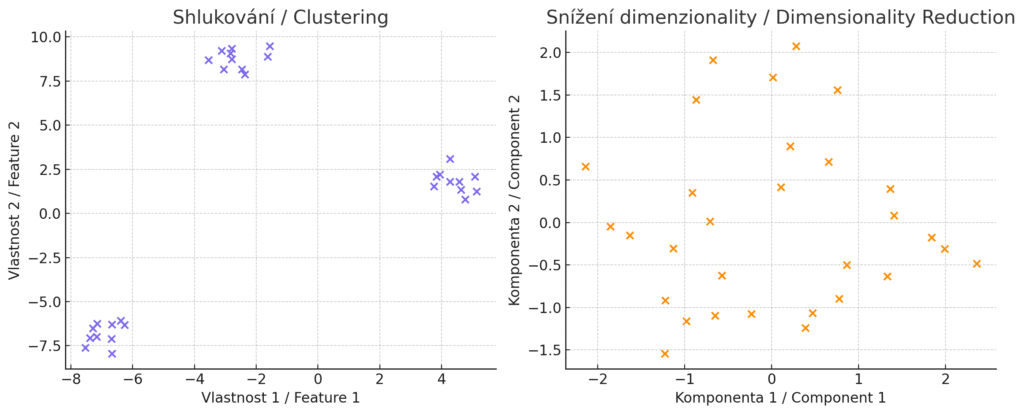
Při hodnocení výkonu všech algoritmů je klíčové použít křížovou validaci – techniku, která rozdělí data na trénovací a testovací část, aby se ověřilo, jak dobře model generalizuje na nová, neviděná data. Tím se předchází přeučení a získává realistický odhad skutečné přesnosti modelu.
Před samotným trénováním je často nutné data předzpracovat. Standardizace nebo normalizace vstupních rysů je kritická pro algoritmy citlivé na měřítko (KNN, SVM, neuronové sítě, PCA), zatímco stromové algoritmy si s různými škálami poradí bez úprav. Další časté kroky zahrnují řešení chybějících hodnot a transformaci kategoriálních proměnných.
Při trénování modelů se setkáváme s dvěma základními problémy: přeučení (overfitting) nastává, když se model naučí trénovací data příliš detailně včetně šumu a nedokáže dobře generalizovat na nová data. Naopak podučení (underfitting) znamená, že model je příliš jednoduchý a nedokáže zachytit ani základní vzory v datech.
Tyto problémy souvisí s fundamentálním kompromisem mezi vychýlením a rozptylem (bias-variance tradeoff). Pro zmírnění přeučení se často využívají regulační techniky (regularizace), které omezují složitost modelu. Jednoduché modely mají obvykle vysoké vychýlení (bias) ale nízký rozptyl (variance) – jsou stabilní, ale mohou být příliš zjednodušující. Komplexní modely mají nízké vychýlení ale vysoký rozptyl – dokážou zachytit složité vzory, ale jsou citlivé na změny v trénovacích datech.
Pro hodnocení modelů existuje mnoho metrik kromě obecné „přesnosti“. U Klasifikace se používají precision, recall, F1-skóre nebo ROC AUC, u Regrese pak MAE, MSE nebo R². Volba metriky závisí na povaze problému – například u nevyvážených dat může být accuracy zavádějící.
Níže uvádíme nejčastější algoritmy jejich popis a příklady použití.
Logistická regrese (Logistic Regression)
Logistická Regrese je jednoduchý lineární algoritmus používaný převážně pro binární klasifikaci (dvojtřídové problémy). Model odhaduje pravděpodobnost příslušnosti ke třídě pomocí logistické (sigmoidní) funkce. V praxi se logistická Regrese využívá například pro klasifikaci emailů jako spam/ham, predikci zákaznického odlivu (zda zákazník odejde), nebo lékařské diagnostické testy (pravděpodobnost onemocnění na základě příznaků). Díky svému lineárnímu charakteru je rychlá a dobře škáluje i na velké datasety. Model je také dobře interpretovatelný – každý vstupní rys má koeficient vyjadřující jeho vliv na výsledek, což umožňuje pochopit, jak model ke svému rozhodnutí došel.
| Výhody | Nevýhody |
| Logistická Regrese je snadno implementovatelná a srozumitelná. Poskytuje jasný pravděpodobnostní výstup (např. „s pravděpodobností 90 % je email spam“). Z výpočetního hlediska jde o velmi efektivní algoritmus – trénování je rychlé a nevyžaduje velké výpočetní zdroje. Má menší kapacitu pro přeučení než složitější modely, ale při vysokém počtu rysů relativně k vzorkům nebo silně korelovaných rysech se může přeučit. Regularizace (L1/L2) tento problém výrazně snižuje. | Hlavním omezením je předpoklad linearity – logistická Regrese předpokládá lineární vztah mezi vstupními rysy a log-odds (logaritmus poměru pravděpodobností), což znamená, že data by měla být lineárně separovatelná (oddělitelná hyperrovinou). V mnoha reálných úlohách tento předpoklad neplatí.Model tedy nedokáže zachytit složitější nelineární vztahy mezi vstupy a výstupem. Dále může nastat problém, pokud je počet rysů (featureů) výrazně větší než počet trénovacích vzorků – v takovém případě model může přeučit na trénovací data. Logistická Regrese také neumí přímo řešit vícetřídové úlohy (musí se použít buď jedna-vs-ostatní schémata, nebo softmax regresi pro více tříd). |
Typické použití logistické Regrese
Klasifikace binárních událostí jako například spam filtry (spam vs. legitimní email – ham), detekce podvodných transakcí (podvod ano/ne). Vhodný je i na predikce pravděpodobnosti, jako jsou modelování rizika v pojišťovnictví či financích (pravděpodobnost nesplácení úvěru). Využívají se také v medicíně při úlohách v diagnostice, např. pravděpodobnost pozitivního nálezu na základě testů.
Logistická Regrese často slouží jako výchozí základní model (baseline) pro porovnání s pokročilejšími algoritmy díky své jednoduchosti a interpretovatelnosti.)
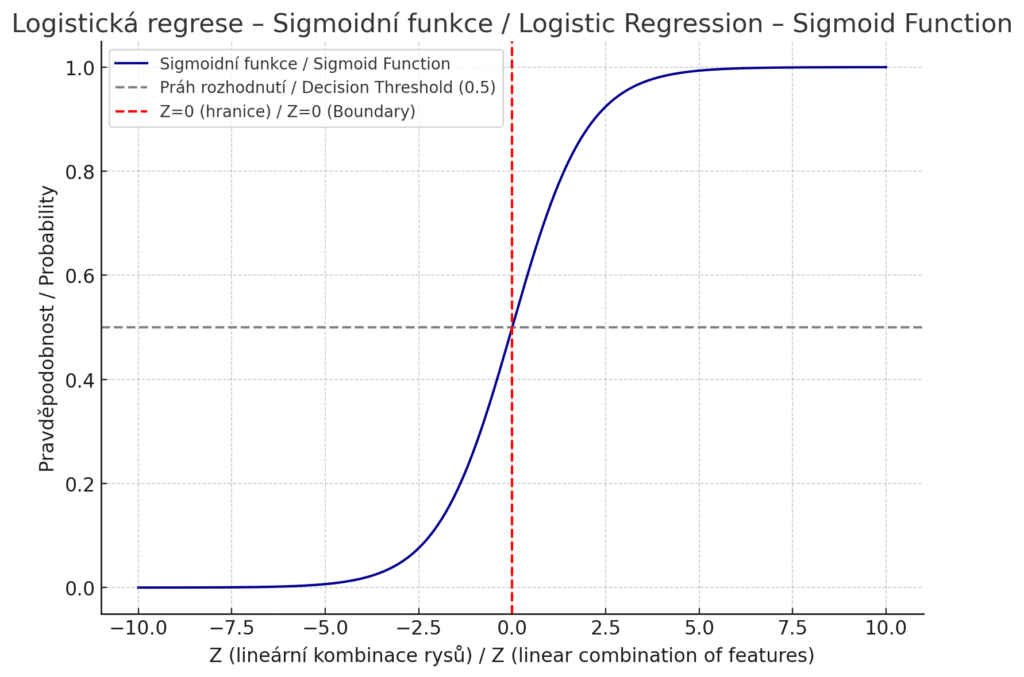
Graf sigmoidní funkce, která tvoří základ rozhodování u logistické Regrese. Zobrazuje, jak se lineární výstup modelu (osa X) převádí na pravděpodobnost (osa Y).
Lineární Regrese (Linear Regression)
Lineární Regrese je základní algoritmus pro regresní úlohy, který modeluje vztah mezi vstupními rysy a spojitou cílovou proměnnou pomocí lineární funkce. Na rozdíl od logistické Regrese, která predikuje pravděpodobnosti kategorií, lineární Regrese přímo odhaduje číselnou hodnotu výstupu jako vážený součet vstupních rysů plus konstantu (intercept). Matematicky se zapisuje jako y = β₀ + β₁x₁ + β₂x₂ + … + βₙxₙ, kde β koeficienty se učí z trénovacích dat metodou nejmenších čtverců. Lineární Regrese se široce využívá pro predikci cen (nemovitosti, akcie), odhady prodejů, analýzu vlivu marketingových kampaní na tržby, nebo v ekonomii pro modelování vztahů mezi makroekonomickými ukazateli. Díky své jednoduchosti bývá prvním krokem při analýze dat a slouží jako baseline pro porovnání se složitějšími modely díky své jednoduchosti a interpretovatelnosti.
| Výhody | Nevýhody |
| Lineární Regrese patří k nejrychlejším algoritmům – trénování i predikce jsou extrémně rychlé díky analytickému řešení (není třeba iterativní optimalizace). Koeficienty β mají přímý interpretační význam – ukazují, o kolik se změní výstup při zvýšení daného rysu o jednotku. Model je robustní vůči přeučení, zejména při použití regularizace (Ridge nebo Lasso Regrese). Dobře škáluje na velká data a nevyžaduje složité nastavení hyperparametrů. Poskytuje také statistické informace o spolehlivosti odhadů (p-hodnoty, intervaly spolehlivosti). | Hlavním omezením je předpoklad linearity – model dokáže zachytit pouze lineární vztahy mezi vstupy a výstupem, což v mnoha reálných situacích neplatí. Lineární Regrese je citlivá na odlehlé hodnoty, které mohou výrazně zkreslit koeficienty. Předpokládá homoskedasticitu (konstantní rozptyl chyb) a normalitu residuí pro správné statistické inference. Při vysokém počtu rysů relativně k počtu vzorků může docházet k přeučení. Model také trpí multikolinearitou – silně korelované vstupní rysy mohou způsobit nestabilní odhady koeficientů. |
Typické použití lineární Regrese
Lineární Regrese je ideální pro predikci spojitých hodnot, kde předpokládáme přibližně lineární vztahy. Častým využitím je odhad cen nemovitostí na základě rozlohy, lokality a stáří budovy, predikce prodejů na základě marketingových výdajů a sezónních faktorů, nebo analýza vlivu různých faktorů na mzdy zaměstnanců. V ekonomii se používá pro modelování vztahů mezi HDP, inflací a nezaměstnaností. Ve vědeckém výzkumu pomáhá kvantifikovat vztahy mezi proměnnými – například vliv teploty na růst rostlin. Pokud lineární model dosahuje dobrých výsledků, může být lepší volbou než složitější algoritmy kvůli snadnému vysvětlení a nasazení. Pokud linearita nestačí, lze model rozšířit o polynomiální rysy nebo interakce mezi proměnnými, případně přejít ke komplexnějším algoritmům.
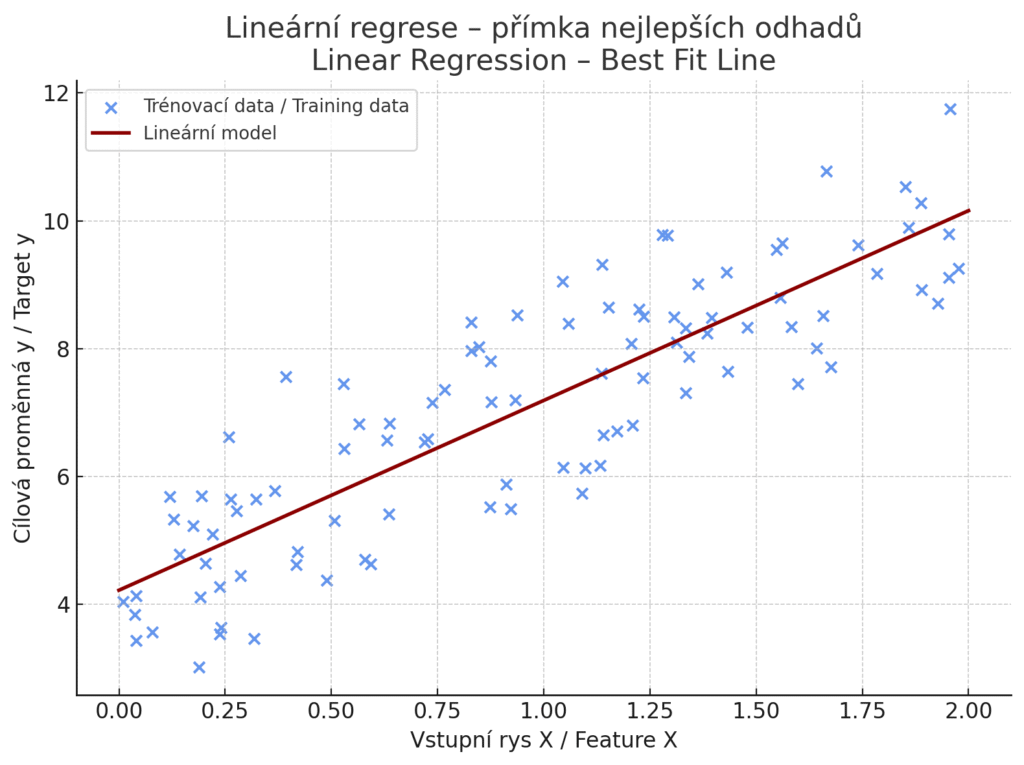
Modré body představují trénovací data – vstupy a odpovídající výstupy. Červená přímka je lineární model ve tvaru y=β0+β1xy = beta_0 + beta_1 xy=β0+β1x, který byl natrénován metodou nejmenších čtverců. Model se snaží minimalizovat celkový čtvercový rozdíl mezi predikcemi a skutečnými hodnotami.
Rozhodovací strom (Decision Tree)
Rozhodovací stromy jsou populární interpretovatelné modely pro klasifikaci i regresi. Strom postupně dělí data podle hodnot vstupních rysů – v uzlech pokládá „rozhodovací otázky“ typu „Je hodnota rysu X > 5?“ a podle odpovědi větví dál. Výsledkem je stromová struktura, kde listy představují konečná rozhodnutí nebo predikce. Rozhodovací strom dokáže zachytit nelineární vztahy mezi vstupními proměnnými a cílem. Díky stromové struktuře je jeho rozhodování snadno vysvětlitelné: lze jej vizualizovat a sledovat cestu od kořene k listu, která představuje rozhodovací pravidla vedoucí k závěru. Toho se využívá pokud je potřeba svá rozhodnutí obhájit – výsledek lze snadno interpretovat a zdůvodnit.
| Výhody | Nevýhody |
| Hlavní výhodou je jednoduchá interpretace výsledného modelu – i netechnický uživatel může sledovat pravidla ve stromu a pochopit, proč model dospěl k dané predikci. Rozhodovací stromy umí pracovat s různými typy vstupů (čísla i kategorie) a nevyžadují škálování rysů. Dokážou si poradit i s nelineárními vztahy a interakcemi mezi proměnnými (na rozdíl od čistě lineárních modelů). Trénování stromu je relativně rychlé i na větších datech, protože algoritmus prohledává rozdělení dat podle jednotlivých rysů a vybírá ty nejinformativnější rozdělovače. | Jednoduchý strom má tendenci přeučit data, pokud se nechá volně růst do velké hloubky. Hloubkové stromy mohou vytvořit velmi specifická pravidla, která platí jen pro trénovací data, a tím ztrácí schopnost generalizace na nová data. Proto se často omezuje hloubka stromu nebo počet vzorků v listech pro zlepšení generalizace. Rozhodovací stromy také trpí vysokou variabilitou – malé změny v datech mohou vést ke zcela jiné struktuře stromu. Samostatný strom mívá nižší predikční přesnost než sofistikovanější metody (například ensemble metody jako náhodný les či boosting, které využívají mnoho stromů). V případě nevyvážených dat (imbalance tříd) mohou stromy upřednostňovat většinovou třídu a zanedbat minoritní třídy. |
Typické použití rozhodovacích stromů
Používá se na rozhodovací procesy, kdy strom může představovat postup, jak se rozhodnout na základě vstupních parametrů (např. schválení půjčky podle příjmu a historie klienta). Využití najde i v medicíně, jako diagnostické stromy pro doporučení léčby na základě symptomů pacienta (snadno interpretovatelné pro lékaře). Vhodné jsou i na rychlou prototypizaci, stromy lze využít pro rychlé explorační analýzy dat – odhalí, které proměnné mají vliv a jaké prahové hodnoty jsou kritické (pomáhají i s výběrem příznaků).
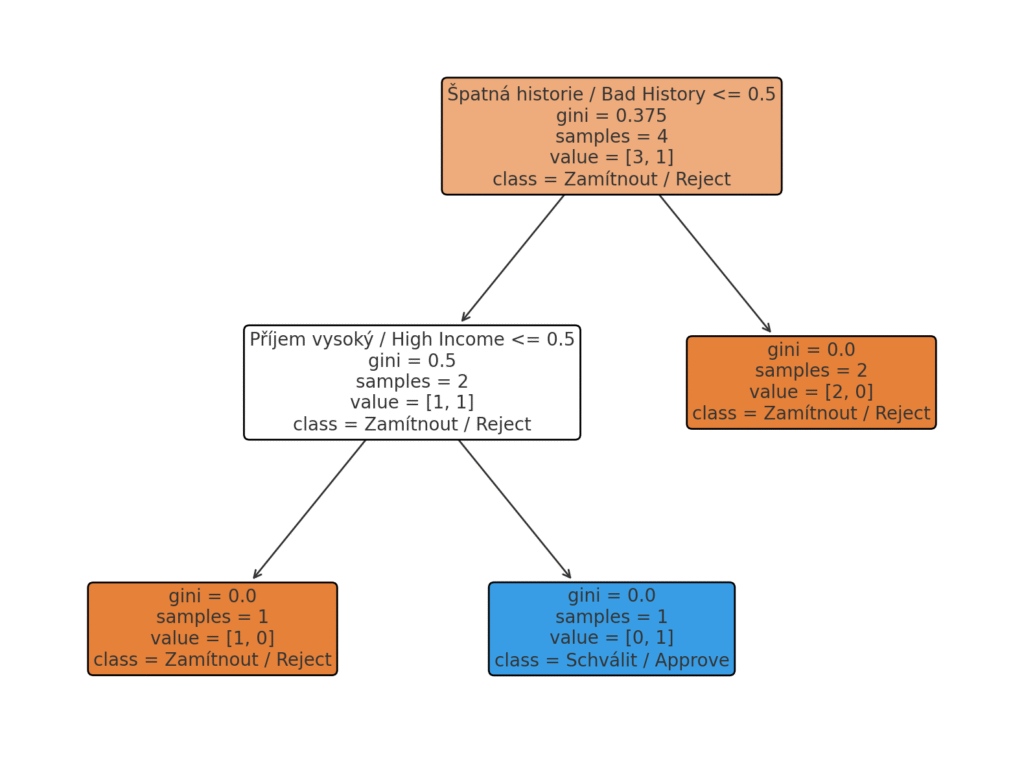
Rozhodovací strom znázorňující proces schvalování půjčky na základě dvou vstupních parametrů – příjem: vysoký vs. nízký / úvěrová historie: dobrá vs. špatná. Vizualizace ukazuje, jak strom pokládá rozhodovací otázky a dospívá ke konečnému rozhodnutí – schválit nebo zamítnout.
Náhodný les (Random Forest)
Náhodný les (Random Forest) je ensemble metoda stavějící na rozhodovacích stromech. Místo jediného stromu algoritmus trénuje velké množství stromů (les) na různých podmnožinách dat a výběrech vlastností. Každý strom v lese hlasuje pro svůj výsledek a náhodný les rozhodne většinovým hlasováním (Klasifikace) nebo průměrem predikcí (Regrese). Tento princip baggingu (bootstrap aggregating) s náhodným výběrem rysů zajišťuje, že stromy budou vzájemně různorodé a model nebude tak snadno přeučený jako jeden hluboký strom. Díky kombinaci mnoha stromů náhodný les obvykle dosahuje vysoké přesnosti a je robustní vůči šumu v datech.
| Výhody | Nevýhody |
| Náhodný les typicky poskytuje velmi přesné predikce díky zprůměrování mnoha modelů – tím snižuje jejich rozptyl a zlepšuje generalizaci. Je odolný vůči šumu a odlehlým hodnotám v datech; jednotlivé stromy se mohou na část šumu nachytat, ale většina stromů přehlasuje případné chybné učící vzory. Model umí odhadnout důležitost rysů – z frekvence či zhoršení chyby po permutaci rysu lze usuzovat, které vstupy jsou pro predikci nejvýznamnější. To je cenné pro interpretaci na úrovni celého datasetu (i když samotný proces rozhodování jednotlivých predikcí není tak průhledný jako u jednoho stromu). | Interpretovatelnost náhodného lesa je omezená – obsahuje stovky až tisíce stromů, které již člověk nemůže snadno celé prozkoumat (lze ale využít např. důležitost rysů – feature importance, či sledovat jednotlivé stromy). Výpočetní náročnost je vyšší než u jednoho stromu, zejména během trénování – model trénuje mnoho stromů (např. 100 nebo 1000) a to vyžaduje více času a paměti. Při nasazení (inference) musí model vyhodnotit každý nový příklad ve všech stromech, což může být pomalejší (ale stále lze paralelizovat, protože výpočet v různých stromech je nezávislý). U velmi velkých datasetů (miliony vzorků) se trénování náhodného lesa může stát zdlouhavé a paměťově náročné – v těchto případech se často volí efektivnější boosting algoritmy. Klíčové hyperparametry zahrnují počet stromů (n_estimators), maximální hloubku stromů (max_depth) a počet rysů pro každé rozdělení (max_features). |
Typické použití náhodných stromů
Je to zejména predikce na strukturovaných datech. Náhodný les je oblíbený výchozí algoritmus pro tabulková data v oblastech, jako jsou finanční modely, predikce v průmyslu, bioinformatika (např. predikce nemocí z genomických dat) apod. Pokud řešíte úlohy s množstvím rysů, pak díky zabudované odhadnuté důležitosti rysů se používá pro výběr nejvlivnějších vstupů. Např. v medicíně pomáhá určit, které faktory (symptomy, laboratorní hodnoty) nejvíce ovlivňují diagnózu. Dalším polem využití jsou aplikace vyžadující robustnost, např. v prostředí s šumem nebo chybějícími údaji (např. senzory IoT s výpadky) náhodný les díky průměrování lépe odolá nekvalitním datům.
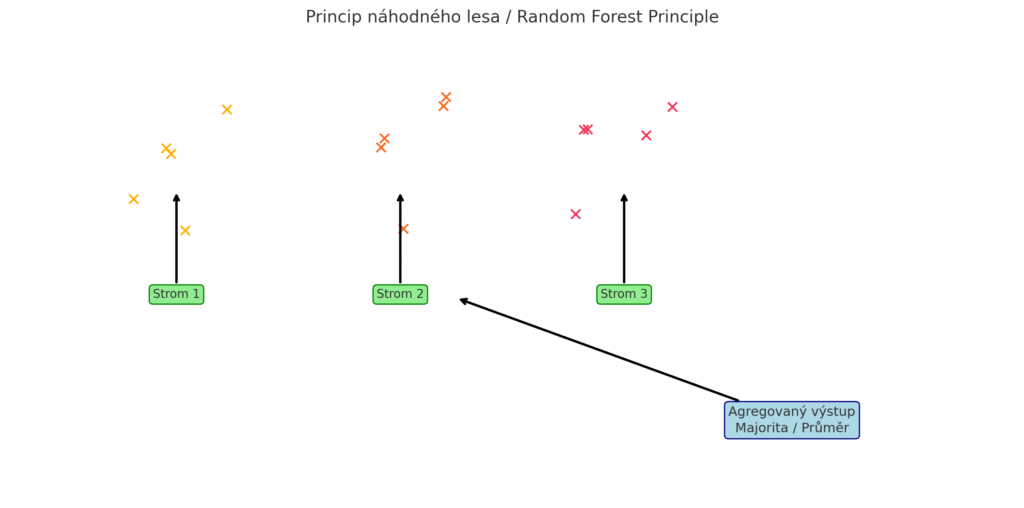
Princip fungování náhodného lesa (Random Forest) – tři náhodné bootstrap vzorky dat (nahoře), tři trénované stromy, každý s jiným pohledem na data, agregace výstupu hlasováním nebo průměrováním.
Algoritmus nejbližších sousedů (K-Nearest Neighbors, KNN)
K-Nearest Neighbors je jednoduchý paměťový algoritmus, který pro nový vstup hledá nejbližší trénovací příklady v prostoru rysů a na základě jejich hodnot odvodí predikci. U Klasifikace nechá nový bod „hlasovat“ mezi jeho k nejbližšími sousedy: přiřadí mu třídu, která je medzi sousedy nejčastější. U Regrese se často bere průměr hodnot sousedů. KNN je tzv. líný učící se algoritmus (lazy learning) – neprobíhá žádná explicitní fáze trénování, model si pouze pamatuje trénovací data. To znamená, že nové vzorky lze přidat snadno bez nutnosti přeučovat celý model.
| Výhody | Nevýhody |
| Metoda k nejbližších sousedů je konceptuálně jednoduchá a snadno pochopitelná. Nevyžaduje složité optimalizační procesy – pro nový bod stačí spočítat vzdálenosti k trénovacím bodům. Díky absenci explicitního trénování se neučí parametry, ale volba k funguje jako regulační mechanismus – malé k (zejména k=1) vede k vysoké varianci a přeučení na lokální šum, velké k snižuje variabilitu, ale může způsobit příliš hladké hranice. KNN je flexibilní – dokáže řešit vícetřídové Klasifikace a různými metrikami vzdálenosti (Euklidovská, Manhattan, Minkowski) lze přizpůsobit jeho chování konkrétnímu problému. Lze jej využít i pro doporučovací systémy (např. doporučení produktu uživateli na základě podobnosti s jinými uživateli). | Výpočetní náročnost při nasazení dramaticky roste s velikostí trénovací množiny. Pokud máme tisíce či miliony trénovacích bodů, nalezení nejbližších sousedů pro každý dotaz může být pomalé (je třeba spočítat vzdálenost ke všem bodům). Existují sice urychlující struktury (např. k-d strom), ale ve vysokých dimenzích se jejich přínos stírá. Model navíc vyžaduje uložení celých trénovacích dat v paměti, což může být náročné. KNN je také citlivý na škálování a šum – různé rozsahy vlastností ovlivní metriky vzdálenosti (nutnost normalizace vstupů) a odlehlé či šumové body mohou mít neúměrný vliv na predikci. KKNN rozhoduje většinovým hlasováním sousedů, přičemž k=1 znamená nulovou trénovací chybu (vzorec si „pamatuje“ každý trénovací bod), což vede k přeučení na lokální šum. Naopak velké k může rozmazat hranice mezi třídami. |
Typické použití K-Nearest Neighbors
Například Klasifikace obrázků či vzorů při malých datasetech – nový obrázek lze klasifikovat podle toho, ke kterým známým obrázkům má nejblíže ve vlastnostech (barvy, textury apod.). Využívá se v doporučovacích systémech (Spotify, Netflix, doporučování produktů na eshopu), a to proto, že KNN lze aplikovat na matici uživatelů a položek – najít „nejbližší“ uživatele s podobným vkusem a doporučit položky, které oblíbil soused, nebo analogicky s položkami (tzv. user-based nebo item-based collaborative filtering). Využívá se i na různé anomálie a detekce outlierů – body, které nemají žádné blízké sousedy (vzdálenosti k nejbližším jsou vysoké), lze považovat za odlehlé či podezřelé (např. detekce podvodů).
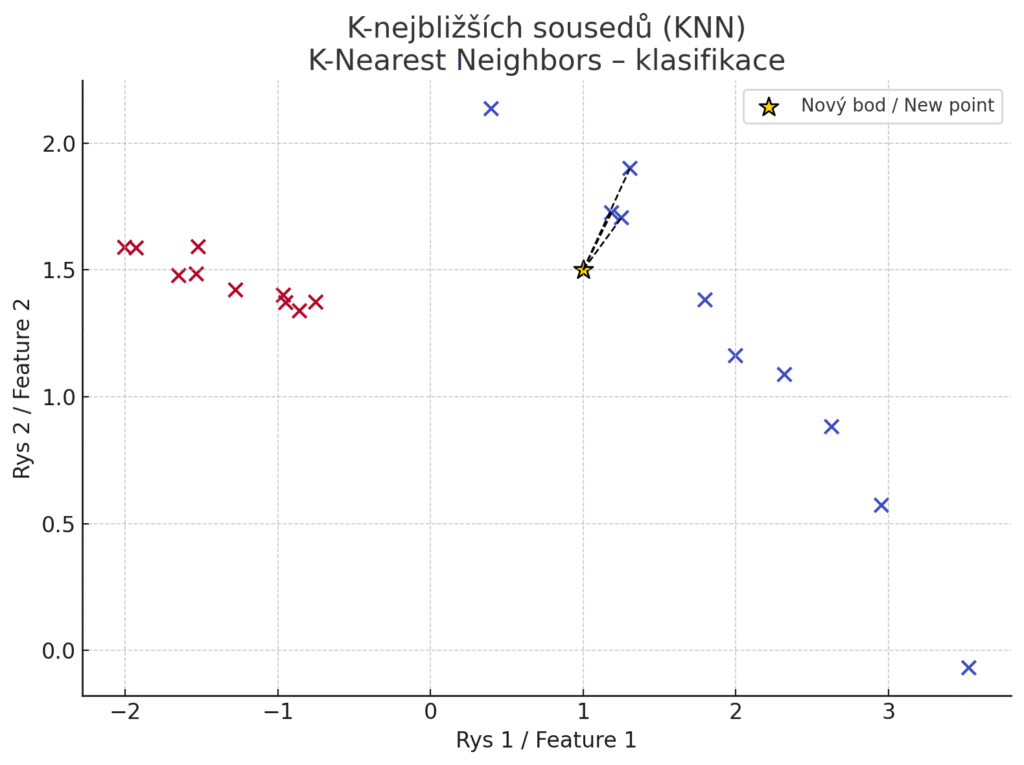
Jednoduchá vizualizace principu K-nejbližších sousedů (K-Nearest Neighbors) v grafu – barevné body jsou trénovací vzorky, zlatá hvězda je nový bod, který chceme klasifikovat a čárkované čáry spojují nový bod s jeho třemi nejbližšími sousedy.
Support Vector Machine (SVM, stroj s podpůrnými vektory)
Support Vector Machine (SVM) je silný algoritmus pro klasifikaci (a také regresi) známý tím, že hledá tzv. optimální hyperrovinu oddělující třídy. Cílem SVM je maximalizovat margin – tedy vzdálenost nejbližších trénovacích bodů od dělící roviny. Intuitivně se snaží najít takovou hranici, která nejlépe odděluje třídy a zároveň má od obou tříd co největší odstup, čímž zlepšuje generalizaci. Klíčovou vlastností SVM je podpora jádrových funkcí (kernel trick), které umožňují transformovat vstupní data do vyšších dimenzí, kde jsou lépe lineárně oddělitelná. Tím SVM zvládá i nelineární klasifikaci, pokud zvolíme vhodné jádro (např. RBF, polynomialní aj.). SVM bylo populární zejména v éře před nástupem hlubokého učení – dosahovalo špičkových výsledků v rozpoznávání obrazů (známá aplikace je Klasifikace ručně psaných číslic) a v textové klasifikaci.
| Výhody | Nevýhody |
SVM je efektivní ve vysokodimenzionálních prostorech při malém počtu vzorků - trénink škáluje O(n²) až O(n³), takže dobře funguje když je počet rysů vysoký relativně k počtu vzorků. Pro miliony vzorků je však nepoužitelné. Má také dobrou schopnost generalizace; díky maximalizaci marginu není tak náchylné k přeučení jako například rozhodovací strom SVM s vhodným jádrem může dosáhnout vysoké přesnosti i na komplexních úlohách, zejména pokud je k dispozici středně velký dataset. Je univerzální – umožňuje různá jádra a tím pádem řešení různorodých problémů (lineární separace, nelineární hranice, s vhodným jádrem i problémy jako sekvenční data atd.). | Trénování SVM je výpočetně náročné, zejména pro velké datasety. Klasický SVM řeší kvadratickou optimalizaci, která škáluje O(n²) až O(n³) s počtem vzorků – pro desítky tisíc či více vzorků může být natrénování velmi pomalé. Existují lineární varianty SVM a stochastické metody, které škálují lépe, ale pro nelineární jádra je to limitace. SVM také vyžaduje ladění hyperparametrů – výběr vhodného jádra a parametrů (např. regulační parametr C, parametr gamma u RBF jádra) není triviální a špatná volba může výrazně zhoršit výkon. Interpretovatelnost SVM je omezená – u lineárního SVM se dají interpretovat váhy podobně jako u logistické Regrese, ale u nelineárních SVM v kernelovém prostoru je model vnímán jako černá skříňka. Navíc výsledné rozhodovací funkce SVM jsou určeny tzv. podpůrnými vektory (podmnožinou trénovacích bodů), jejichž kombinace definuje hranici, což opět znesnadňuje vysvětlení predikce. |
Typické použití Support Vector Machine
SVM (často lineární SVM) se úspěšně používá pro kategorizaci textových dokumentů (spam detekce, třídění článků podle tématu) díky schopnosti pracovat s mnoha atributy (slovy). Před nástupem hlubokých neuronových sítí byly SVM s nelineárním jádrem špičkou např. v rozpoznávání rukopisu (známá data MNIST) či detekci objektů na obrázcích. Současně nachází uplatnění při analýze genetických dat nebo klasifikaci proteinů, kde jsou datové body ve velmi vysoké dimenzi a je třeba robustní klasifikátor pro malé množství trénovacích vzorků.
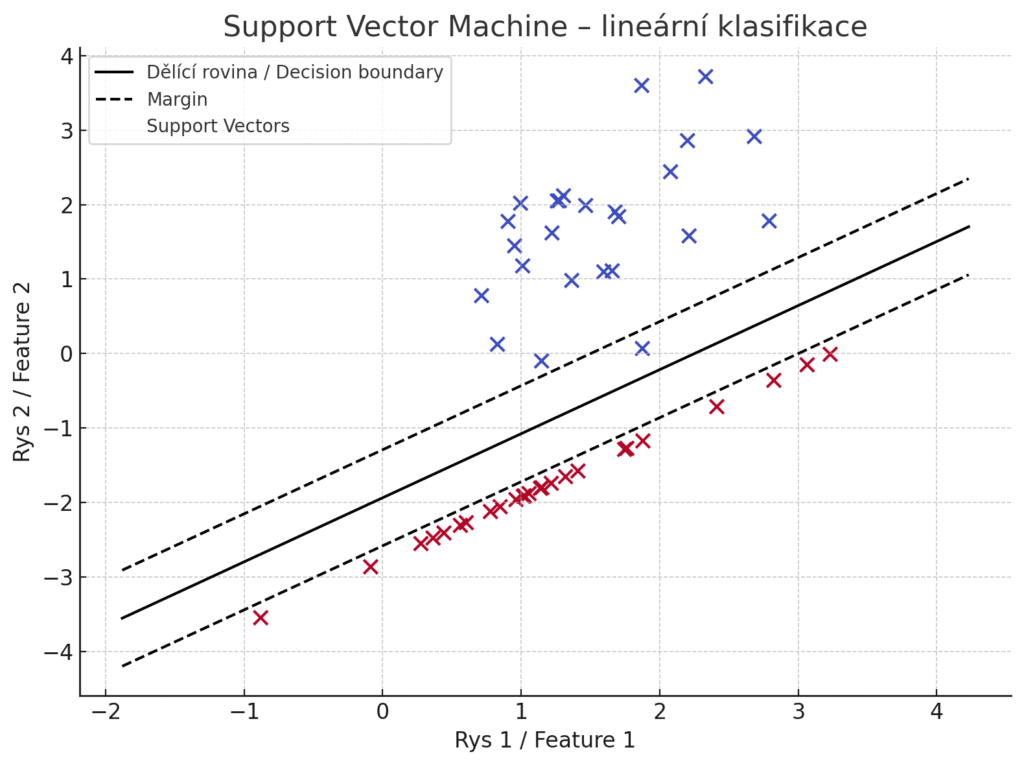
Vizualizace principu Support Vector Machine (SVM) s lineárním jádrem – černá čára je optimální dělící rovina, přerušované čáry znázorňují okraje marginu, prázdné body s černým okrajem jsou support vectors – vzory, které určují polohu rozhodovací hranice.
Naivní Bayesův klasifikátor (Naive Bayes)
Naivní Bayes je jednoduchý pravděpodobnostní klasifikátor založený na Bayesově větě. Označuje se jako „naivní“, protože činí silný (a často nereálný) předpoklad, že vstupní rysy jsou podmíněně nezávislé v rámci každé třídy. V praxi existuje několik variant (multinomální, Bernoulliho, Gaussovský naivní Bayes) podle toho, jaký typ dat zpracovávají. I přes zjednodušující předpoklady bývá naivní Bayes překvapivě účinný hlavně u textových dat. Při klasifikaci dokumentů (např. spam filtry, analýza sentimentu) funguje slušně, protože slova v dokumentu mohou být považována za víceméně nezávislá vzhledem k třídě (např. spam emails často obsahují určitá slova nezávisle na sobě). Model spočítá z trénovacích dat pravděpodobnosti výskytu rysů (slov) v jednotlivých třídách a při predikci vybere tu třídu, pro niž je kombinace rysů nejpravděpodobnější.
| Výhody | Nevýhody |
| Naivní Bayes je velmi rychlý při trénování i predikci – v podstatě stačí projít trénovací data a spočítat četnosti výskytu kombinací rysů a tříd. Díky tomuto je nenáročný na výpočetní výkon a může snadno škálovat na velké objemy dat. Překvapivě dobře funguje i s málo trénovacími daty, pokud se náhodou přibližně splňuje předpoklad nezávislosti – dokáže generalizovat i z několika příkladů díky zakomponování apriorních pravděpodobností. Problémy s mnoha vstupními rysy (např. tisíce slov v textu) mu nevadí, naopak patří mezi algoritmy, které si s vysokou dimenzionalitou poradí (často lépe než složitější modely). | Hlavní nevýhodou je již zmíněný předpoklad nezávislosti rysů – v reálných datech rysy typicky nebývají úplně nezávislé a naivní Bayes tak neví, jak zohlednit jejich závislosti. To může vést k méně přesným predikcím, pokud jsou korelace mezi vstupy důležité. Další praktický problém je tzv. zero-frequency jev: pokud se v trénovacích datech vůbec nevyskytne určitá kombinace rysu a třídy, model jí dá nulovou pravděpodobnost, což pak znemožní (vynuluje) pravděpodobnost celé predikce. Řešením je použít tzv. vyhlazování (smoothing), které do četností přidá malou konstantu a zabrání nulovým pravděpodobnostem. Naivní Bayes také není dobrý odhadce samotných pravděpodobností – jeho výstupní pravděpodobnosti nebývají kalibrované (často je příliš jistý), hodí se spíše jen pro určení nejpravděpodobnější třídy. Interpretace modelu je sice možná z pohledu pravděpodobností (můžeme nahlédnout, které rysy jsou pro danou třídu nejvýznamnější – např. které slovo nejvíce „signalizuje“ spam), ale kvůli předpokladu nezávislosti může být zavádějící a není tak přímočará jako např. u rozhodovacího stromu. |
Typické použití Naive Bayes
Naivní Bayes byl historicky jádrem mnoha spam filtrů, využívá se i pro třídění článků, emailů nebo zpráv podle tématu či sentimentu. Díky rychlosti je vhodný tam, kde je potřeba okamžitě rozhodovat – např. filtrování škodlivých webových stránek v prohlížeči, detekce nevhodných komentářů atd., zvláště pokud jsou vstupy reprezentovány jednoduše (např. vektory slov). Protože přirozeně podporuje více tříd, lze jej tedy použít i tam, kde máme desítky kategorií (například třídění novinových článků do rubrik).
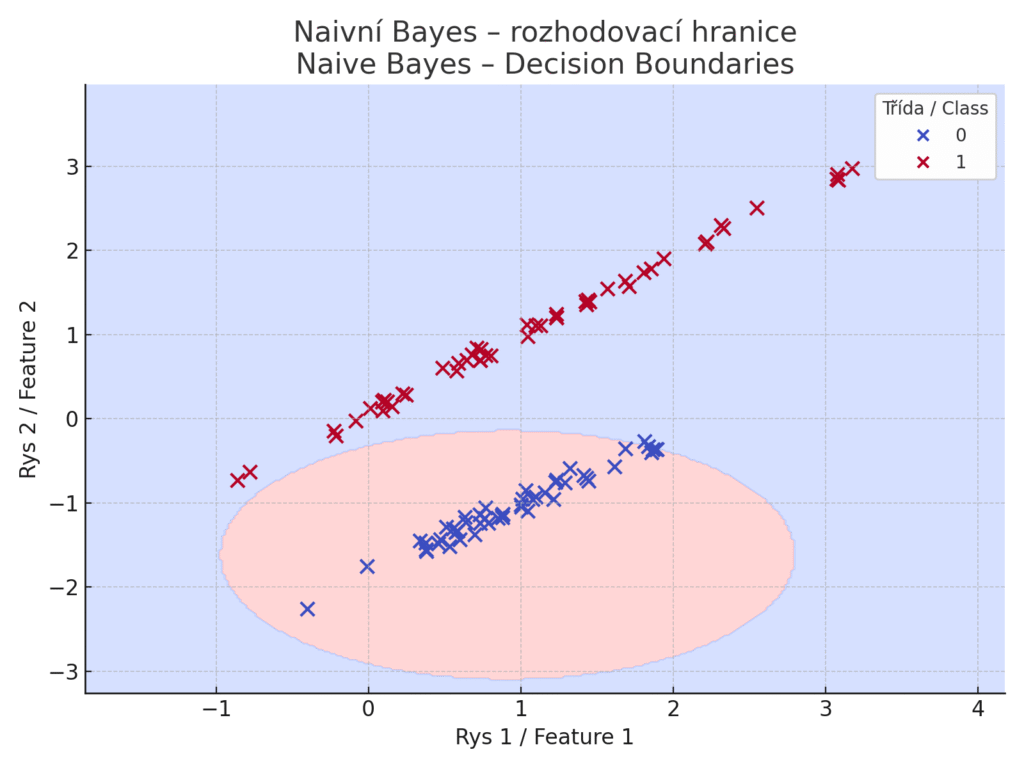
Model očekává, že každý rys má normální rozdělení v rámci každé třídy a že rysy jsou na sobě nezávislé. Modrá oblast – model by pro jakýkoli bod v této oblasti předpověděl Třídu 1 (např. „pozitivní“, „spam“, „ano“…). Barevné oblasti znázorňují rozhodovací hranice, které vycházejí z výpočtu pravděpodobností. Body reprezentují trénovací vzory dvou tříd. Červená oblast – model by pro bod v této oblasti předpověděl Třídu 0 (např. „negativní“, „ham“, „ne“…). Na rozdíl od např. rozhodovacích stromů nebo lineární Regrese nemá Naivní Bayes ostré přímkové hranice, protože rozhoduje na základě spojité pravděpodobnosti – a Gaussovské rozdělení je zvonovité.
Umělé neuronové sítě (Artificial Neural Networks, ANN)
Umělé neuronové sítě (ANN) představují celou rodinu modelů inspirovaných fungováním mozku. Skládají se z propojených neuronů (uzlů) uspořádaných do vrstev. Hluboké neuronové sítě (deep learning) mají více skrytých vrstev, což jim umožňuje naučit se velmi složité funkce.
Mezi populární architektury patří dopředné sítě (feed-forward, využívané pro tabulární data), konvoluční neuronové sítě (CNN) pro zpracování obrazů, nebo rekurentní sítě (RNN) a transformery pro sekvenční data (např. text, časové řady). Neuronové sítě vynikají ve učení reprezentací – dokážou automaticky extrahovat a zkombinovat vhodné příznaky z dat ve skrytých vrstvách. Díky tomu dosahují špičkové přesnosti v mnoha úlohách, pokud je k dispozici dostatek dat. Například v rozpoznávání obrazu a zvuku dnes hluboké sítě výrazně překonávají klasické algoritmy; jsou základem pro technologie jako jsou samořízená auta (rozpoznávání okolí kamerami, LIDARy), hlasoví asistenti (rozpoznání řeči, strojový překlad) nebo detekce objektů na videu.
| Výhody | Nevýhody |
| Umělé sítě patří k nejvýkonnějším modelům z hlediska predikční přesnosti. Dokáží se naučit velmi složité nelineární vztahy v datech, které by jiné algoritmy nezachytily. Jsou univerzální – při dostatečně velké síti lze teoreticky aproximovat libovolnou funkci (universal approximation theorem). V mnoha doménách drží neuronové sítě současné rekordy; např. CNN v počítačovém vidění pro klasifikaci obrázků (ImageNet) nebo transformerové modely v NLP (překlad, jazykové modely). Další výhodou je, že síť se učí přímo z dat surové reprezentace – například v rozpoznávání obrazu odpadá nutnost ručně navrhovat příznaky, síť se sama naučí detekovat hrany, tvary, objekty v různých vrstvách. Škálovatelnost je další plus: s dostatkem výpočetního výkonu lze trénovat na ohromných datasetech a model zlepšovat (výkonný hardware jako GPU/TPU je však nutností). | Největším úskalím neuronových sítí je potřeba velkého množství trénovacích dat. Sítě mají obrovské množství parametrů, které se musí naučit – např. moderní hluboké modely mají miliony až miliardy vah. Pokud bychom je trénovali na malém datasetu, téměř jistě by se přeučily. Proto se využívají hlavně tam, kde jsou k dispozici rozsáhlé datové sady nebo se dají použít předtrénované modely. Výpočetní náročnost je rovněž velmi vysoká: trénování hluboké sítě může trvat hodiny až týdny na výkonných grafických kartách. Nasazení (inference) může být také pomalé, obzvlášť u velkých modelů, což ale lze zlepšit optimalizacemi a specializovaným hardwarem (akcelerátory). Interpretovatelnost neuronových sítí je nízká – jedná se o typickou „černou skříňku“, kde miliony parametrů nemají pro člověka srozumitelný význam. Existují sice metody vysvětlování (např. vizualizace aktivací, LIME, SHAP), které mohou poskytnout jistý vhled, ale obecně je velmi obtížné vysvětlit, proč síť udělala konkrétní rozhodnutí. V některých oblastech sítě naráží i na problém stability – drobné změny vstupu mohou způsobit zcela jinou predikci (známý příklad jsou adversariální příklady v obrazech, které oklamou i jinak přesné CNN). |
Typické použití neuronových sítí
Neuronové sítě jsou v současnosti známé zejména pro zpracování přirozeného jazyka (NLP). Jazykové modely jako GPT pro predikce textu, strojový překlad, rozpoznávání řeči (převod mluvené řeči na text) – to vše dnes zajišťují hluboké neuronové sítě (RNN, transformery). Dalším použití najdeme v oblasti počítačového vidění, jako Klasifikace objektů na obrázcích (např. rozpoznávání zvířat na fotkách) nebo detekce a segmentace objektů ve videu (např. rozpoznat chodce a auta pro autonomní řízení).
Hodí se i na predikce na tabulárních datech. I v běžných úlohách jako predikce cen, detekce podvodu apod. lze neuronové sítě nasadit, zejména pokud je hodně dat – přesto se zde často využívají i jednodušší modely nebo ensemble jako boosting, které mohou být efektivnější.
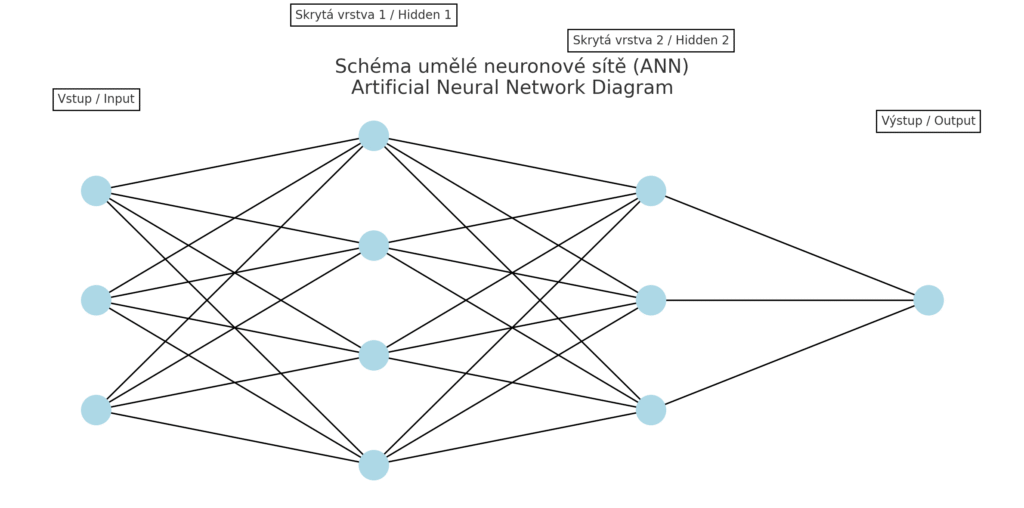
Schéma neuronové sítě ukazuje tři vstupy, dvě skryté vrstvy a jeden výstup. Všechny vrstvy jsou plně propojené – každý neuron je spojen se všemi neurony v další vrstvě. Ilustruje princip dopředné sítě (feed-forward neural network), často používané pro tabulární nebo strukturovaná data.
Shlukování k-means
K-means je nejznámější algoritmus pro shlukovou analýzu (clustering), tedy hledání přirozených skupin v datech bez předem daných kategorií. Cílem k-means je rozdělit data do k shluků tak, aby body v jednom shluku si byly navzájem co nejpodobnější (co nejblíže v prostoru) a zároveň vzdálené od bodů v jiných shlucích. Algoritmus funguje iterativně: náhodně zvolí k počátečních center shluků, přiřadí každý bod k nejbližšímu centru a pak přepočítá centra jako průměr bodů v shluku. Tento proces opakuje, dokud se centra ustálí. Výsledkem jsou souřadnice center (tzv. centroidů) a přiřazení každého bodu k jednomu z nich. Využití k-means je v úlohách, kde chceme objevit latentní skupiny – např. segmentace zákazníků podle nákupního chování, shlukování obrázků podle vizuální podobnosti, seskupení dokumentů s podobnými tématy atd.
| Výhody | Nevýhody |
| K-means je relativně jednoduchý algoritmus s časovou složitostí O(n·k·d·i), kde n je počet bodů, k počet shluků, d dimenze a i iterace. Pro menší až střední data je rychlý, ale při růstu kteréhokoli z parametrů (zejména n nebo k) může být pomalejší. Pro velmi velké datasety se používají optimalizace jako MiniBatch K-means. Při rozumně zvoleném k a inicializaci konverguje během několika iterací (byť hrozí konvergence k lokálnímu minimu). Algoritmus je snadno implementovatelný a pochopitelný, což z něj dělá častou volbu pro úvodní průzkum dat. Pro nové (neviděné) body je přiřazení do shluku velmi snadné a rychlé – stačí spočítat vzdálenost k k centroidům a vybrat nejbližší. | U k-means je nutné předem zvolit počet shluků k, což nemusí být zřejmé a často se zkouší více hodnot. Algoritmus je citlivý na počáteční volbu centroidů – špatná inicializace může vést k horším výsledkům (tomu se částečně předchází chytrou inicializací jako k-means++). Dále k-means funguje nejlépe, pokud shluky mají přibližně kulovitý (konvexní) tvar a podobnou velikost; u dat s nepravidelně tvarovanými shluky může selhávat, protože vždy optimalizuje jen intra-cluster vzdálenosti. Algoritmus je rovněž citlivý na odlehlé body (outliery) – i jeden outlier může značně posunout centroid. Ve vysokodimenzionálních prostorech k-means často trpí tzv. curse of dimensionality – metrika vzdálenosti ztrácí vypovídací schopnost a všechny body mohou být zhruba stejně vzdálené. To snižuje kvalitu shlukování. Interpretace shluků může být náročná: k-means samo neříká, čím jsou shluky charakteristické, jen rozdělí data. Analytik musí dodatečně interpretovat význam nalezených skupin (např. „shluk 1 jsou zákazníci, co nakupují často malé položky“ apod.). |
Typické použití k-means
- Segmentace zákazníků: Na základě dat o chování zákazníků (nákupy, frekvence, demografie) lze pomocí k-means rozdělit zákazníky do skupin pro cílený marketing.
- Zpracování obrazu: K-means se používá pro kvantizaci barev – zvolí se k barev, které nejlépe reprezentují obraz, a ostatní barvy se nahradí nejbližšími centry. Tím lze komprimovat obrázek (nižší počet barev) nebo segmentovat obraz do oblastí podle barvy.
- Inicializace pro jiné algoritmy: Centroidy z k-means mohou posloužit jako výchozí reprezentace dat (např. ve feature learningu), nebo jako počáteční stavy pro složitější modely (např. inicializace center u GMM).
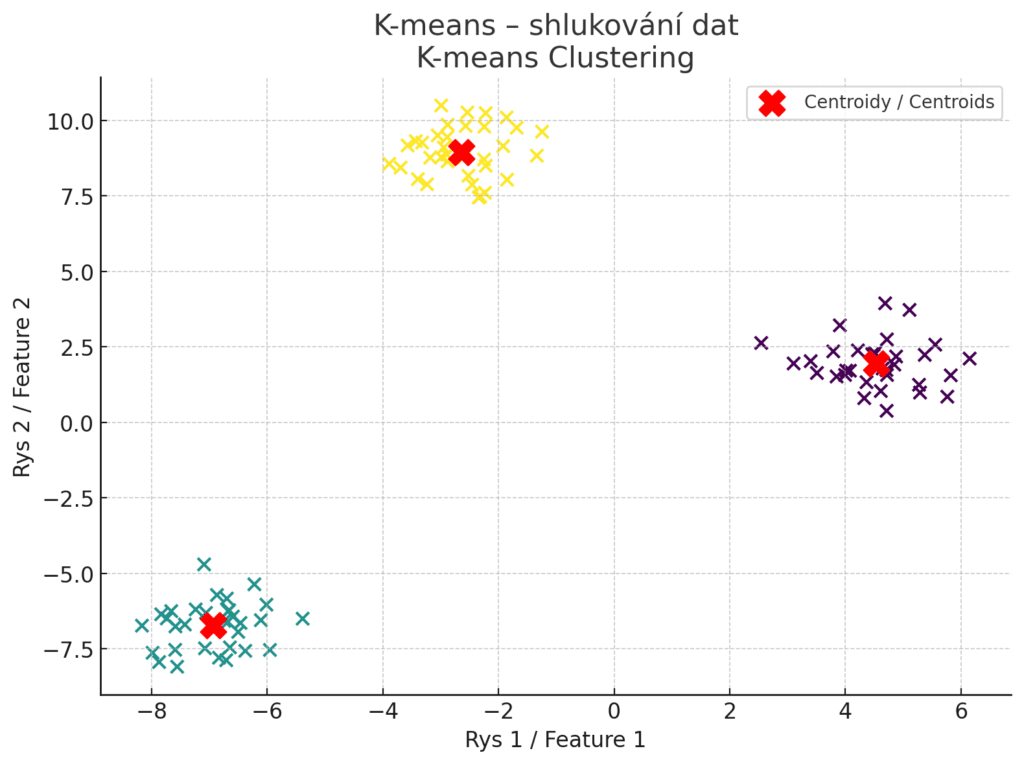
Vizualizace fungování algoritmu K-means. Barevné body znázorňují jednotlivé datové body rozdělené do tří shluků. Červené „X“ značky představují centroidy – průměrné pozice bodů v každém shluku. Každý bod je přiřazen ke svému nejbližšímu centroidu, aby vznikly kompaktní a dobře oddělené skupiny.
Všimli jste si, že na první pohled se algoritmy K-means a K-nearest neighbors (KNN) mohou zdát podobné. Oba se často vizualizují jako body rozprostřené v prostoru, rozdělené podle určité blízkosti nebo příslušnosti k nějaké skupině. V obou případech se navíc mluví o „nejbližších bodech“, „shlucích“ a měření vzdáleností. Jenže pod povrchem jsou tyto dva přístupy zásadně odlišné – jak účelem, tak fungováním i využitím. K-means je algoritmus učení bez učitele (unsupervised learning). Neexistují žádné předem známé třídy nebo kategorie. Cílem je najít přirozené skupiny (shluky) v datech. Algoritmus sám zjišťuje, které body si jsou podobné, a seskupuje je do shluků tak, aby body v jednom shluku byly co nejblíže sobě a co nejdál od bodů v jiných shlucích. KNN naproti tomu patří do učení s učitelem (supervised learning). Pracuje s trénovacími daty, kde každému bodu je známá třída. Při klasifikaci nového bodu se algoritmus podívá, ke kterým známým vzorům je nejblíž, a většinovým hlasováním určí jeho třídu.
Na vizualizacích mohou oba modely působit podobně: data jsou rozdělená v prostoru a barevně označená. Ale:
- K-means rozděluje prostor na základě blízkosti ke středu shluku – oblasti bývají rovnoměrné a symetrické, protože centroidy jsou geometrické průměry.
- KNN rozděluje prostor nerovnoměrně, podle toho, kde se ve skutečnosti nacházejí známé body – hranice jsou často zubaté a složité, protože reagují na konkrétní lokální vzory
Analýza hlavních komponent (Principal Component Analysis, PCA)
Analýza hlavních komponent (PCA) je základní metoda pro snížení dimenzionality dat. Jejím cílem je najít novou sadu ortogonálních proměnných (hlavních komponent), které zachycují co největší možnou variabilitu původních dat. Prakticky jde o nalezení směru v datovém prostoru, ve kterém jsou data nejvíce rozptýlená – to bude první hlavní komponenta. Druhá hlavní komponenta je směr s druhým největším rozptylem, který je zároveň kolmá na první, atd. Projekcí dat do několika prvních komponent tak získáme nižší počet nových rysů, které ovšem stále zachycují většinu informace z původních dat. PCA se hojně využívá jako předzpracování dat – redukcí dimenze lze odstranit šum a redundantní informace, zrychlit následné učení modelů a někdy i zlepšit přesnost (pokud odfiltrovaný šum dříve model mátl). Také se používá pro vizualizaci dat – projekcí vysokodimenzionálních dat do 2D nebo 3D (první dvě či tři komponenty) lze data zobrazit a pozorovat struktury (shluky, odlehlé body).
| Výhody | Nevýhody |
| PCA odstraňuje korelované rysy – nové komponenty jsou lineární kombinace původních rysů, a tím dokáže sloučit informace ze silně korelovaných proměnných do jedné. Tím jednak redukuje redundantní data, jednak může zlepšit výkon některých modelů (např. lineární modely či k-means mohou trpět na multikolinearitu, což PCA eliminuje). Snížením dimenze také omezíme přeučení – model v menším prostoru parametrů nemůže tak snadno přeučit šum. PCA je výpočetně proveditelná i na relativně velkých datech díky efektivním implementacím (např. SVD). Nasazení PCA (projekce nových dat) má časovou složitost O(d × k), kde d je původní dimenze a k počet komponent – při projekci z 1000 rysů do 10 komponent dojde k významnému zrychlení následných výpočtů. | Interpretace hlavních komponent není vždy snadná – každá komponenta je kombinací původních rysů a nemusí mít přímý sémantický význam. Lze však analyzovat, které původní rysy nejvíce přispívají k jednotlivým komponentám (loading vectors), což pomáhá pochopit, co komponenta reprezentuje. Například první komponenta může představovat kombinovaný „všeobecný faktor“ zahrnující více původních veličin, což se těžko popisuje slovy. Při použití PCA také dochází ke ztrátě informace – pokud vybereme jen pár prvních komponent, zbytek rozptylu (byť malý) zanedbáme. To může být problém, pokud zrovna v zanedbané části prostoru leží informace důležitá pro určité vzácné případy. PCA také předpokládá linearitu – hledá lineární kombinace rysů. Pokud jsou důležité spíše nelineární vztahy, existují lepší metody (např. t-SNE, UMAP pro vizualizaci, nebo autoenkodéry v hlubokém učení pro nelineární snížení dimenze). Z praktického hlediska je nutné standardizovat vstupní data před PCA – metrika rozptylu je ovlivněna měřítkem, a rysy s většími číselnými hodnotami by dominovaly výběru komponent. |
Typické použití PCA
Před trénováním složitějších modelů (SVM, neuronové sítě) na datech s mnoha rysy se PCA používá ke snížení dimenze a odfiltrování šumu, čímž se trénování zrychlí a potenciálně zlepší výkon. V genetice PCA pomáhá vizualizovat vysokodimenzionální data jako příbuznost populací (projekce genomických variací do 2D), v ekonomii pro zobrazení trhů, atd. PCA lze použít k kompresi dat – např. pro obraz lze najít hlavní komponenty (vlastní obrazy) a ukládat jen souřadnice bodu v prostoru komponent místo původních pixelů.
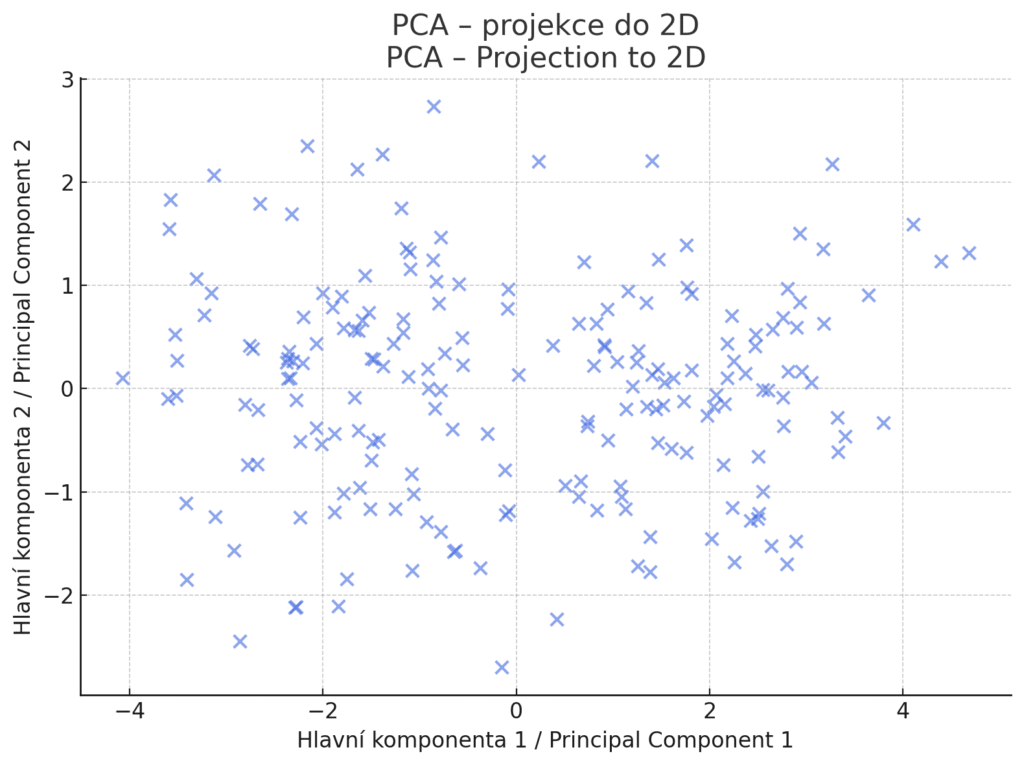
Vizualizace výsledku analýzy hlavních komponent (PCA). Data byla původně ve 5dimenzionálním prostoru. Pomocí PCA byla projekčně zredukována do 2D, přičemž zachovaná osa (PC1 a PC2) reprezentuje dva nejvíce rozptylové směry v datech. Tato vizualizace odhaluje případné shluky, odlehlé body nebo geometrickou strukturu dat v hlavních směrech variability.
Self-Organizing Maps (SOM, Kohonenovy sítě)
Self-Organizing Map (SOM) je specifický typ neuronové sítě navržený pro učení bez učitele, který umožňuje transformaci vysokodimenzionálních dat do dvourozměrné reprezentace. Její síla spočívá nejen v klasifikační nebo shlukovací schopnosti, ale především v tom, že zachovává topologické uspořádání: podobné vzory zůstávají blízko sebe i po projekci. Tím se SOM zásadně liší například od K-means, který sice seskupí podobná data, ale nijak nezachovává vzájemné vztahy v prostoru.
Na vstupu je libovolný počet rysů – např. vektor velikosti 50 může reprezentovat zákazníka, genovou expresi nebo síťový tok. V pozadí je mřížka neuronů (často 2D, např. 10×10), kde každý neuron má váhový vektor stejné délky jako vstupní data. Trénink probíhá opakovaným procházením vstupů, při kterém nejprve najdeme nejbližší neuron (tzv. Best Matching Unit – BMU) pro daný vstupní vektor, potom aktualizujeme váhy tohoto neuronu a jeho okolí tak, aby se přiblížily vstupnímu vzoru a snižujeme vliv okolí a učící rychlost v čase.
Výsledkem je mapa, kde podobné vstupy končí blízko sebe, a tím vzniká přirozená segmentace i prostorová struktura.
| Výhody | Nevýhody |
| Vynikající pro vizualizaci komplexních dat, zachovává topologii, relativně rychlý trénink O(n × epochs), umožňuje snadnou identifikaci shluků a anomálií prostřednictvím heat-map. | Citlivost na volbu rozměru mřížky a počáteční váhy, obtížná interpretace co jednotlivé oblasti mapy představují, méně přesné než specializované clustering algoritmy. Nelze snadno využít pro predikci, je to výhradně nástroj pro exploraci, ne pro učení s učitelem. |
Typické použití Self-Organizing Map
Segmentace zákazníků s vizualizací jejich charakteristik, analýza genomických dat, detekce anomálií v síťovém provozu prostřednictvím heat-map odchylek, explorační analýza vysokodimenzionálních dat před aplikací jiných algoritmů.
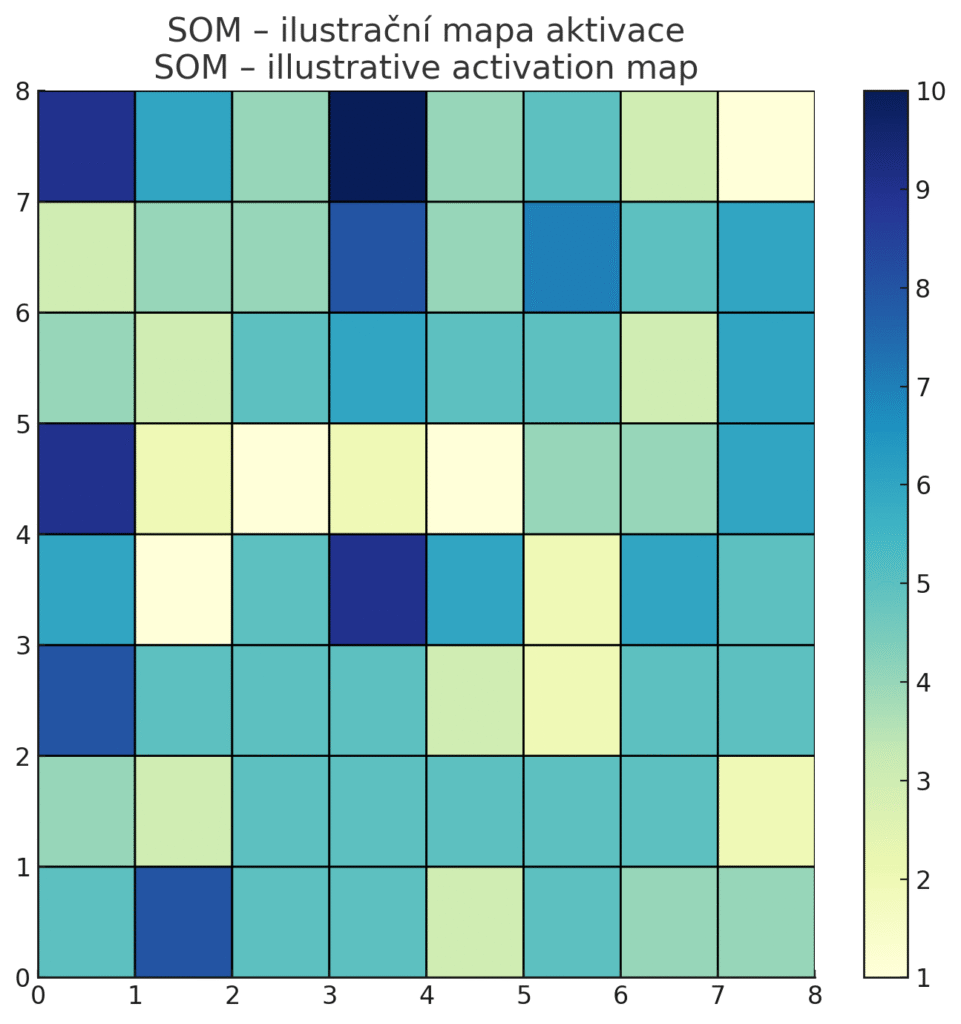
Ilustrační vizualizace Self-Organizing Map (SOM), kde každé pole ve 2D mřížce (8×8) reprezentuje jeden neuron. Intenzita barvy ukazuje, kolik vstupních vzorů „padlo“ do daného neuronu – čím tmavší, tím více datových bodů bylo přiřazeno. Tato mapa pomáhá intuitivně vnímat, kde se nacházejí shluky, husté oblasti i odlehlé oblasti (s nízkou aktivitou).
AdaBoost (Adaptive Boosting)
AdaBoost je první populární algoritmus z rodiny boosting metod. Boosting obecně funguje tak, že sekvenčně přidává ke kombinaci několik jednoduchých modelů (slabých učitelů) a každý nový model se soustředí na chyby předchozích. AdaBoost konkrétně často používá jako slabé učitele jednoduché rozhodovací stromy (tzv. pařezy – stromy hloubky 1 nebo 2). Postupně trénuje například stromek, vyhodnotí chyby, zvýší váhu špatně klasifikovaných vzorků a na dalším stromu se tyto hůře naučitelné případy mají větší vliv. Tak se ensemble „adaptivně“ zlepšuje na těžších příkladech. Finální predikce je pak vážená kombinace všech slabých modelů (u Klasifikace obvykle hlasování vahami α, u Regrese součet). AdaBoost proslul v úloze detekce obličejů na obrázcích (Viola-Jones algoritmus), kde kombinace mnoha jednoduchých pravidel dokázala efektivně detekovat tváře v reálném čase.
| Výhody | Nevýhody |
| AdaBoost typicky zvyšuje přesnost oproti jednomu stromu – kombinací mnoha slabých pravidel lze získat silný model. Je méně náchylný k přeučení než velký hluboký strom, protože slabé učitele regularizuje – každý stromek je velmi jednoduchý a samostatně by měl velkou chybu, ale v kombinaci se chyby kompenzují. V době svého vzniku byl AdaBoost oblíbený pro snadnou implementaci a interpretaci – slabé stromy (pařezy) se daly vizualizovat a váhy α ukazovaly, jakou důležitost jednotlivé stromy mají, což dávalo určitý vhled do modelu. | AdaBoost je citlivý na odlehlé hodnoty – pokud má trénovací data s chybně označenými příklady nebo outliery, bude se je boosting snažit mermomocí naučit (dá jim rostoucí váhu), což může zhoršit celkový výkon. Algoritmus také není triviálně paralelizovatelný, protože nové slabé modely navazují na výsledky předchozích – to může být nevýhoda u opravdu velkých datasetů. V takových případech může trénování trvat dlouho (výpočetní náročnost roste s počtem iterací/slabých modelů). AdaBoost sám o sobě nemá tolik volných parametrů, ale nastavení např. počtu iterací je důležité – příliš mnoho slabých modelů může vést k přeučení, příliš málo zase k podfitování. Dnes byl původní AdaBoost překonán pokročilejšími boosting algoritmy (viz níže), které lépe škálují a jsou odolnější. |
Typické použití AdaBoost
Jak už bylo zmíněno, AdaBoost proslul v detekci obličejů (kombinoval jednoduché Haarovy příznaky). Obecně se dá boosting použít pro jakoukoli detekci objektů, kde se kombinuje mnoho jednoduchých pravidel. AdaBoost lze aplikovat na širokou škálu klasifikačních úloh místo logistické Regrese či SVM, pokud je cílem vyšší přesnost a nevadí delší trénování. V praxi jej však dnes často nahrazuje jeho pokročilejší verze – gradient boosting. V dřívějších strojově učících soutěžích (Kaggle ~2010) byl AdaBoost jedním z ensemble, které šlo zkoušet pro zlepšení přesnosti modelu. Dnes jej zastínily algoritmy jako XGBoost.
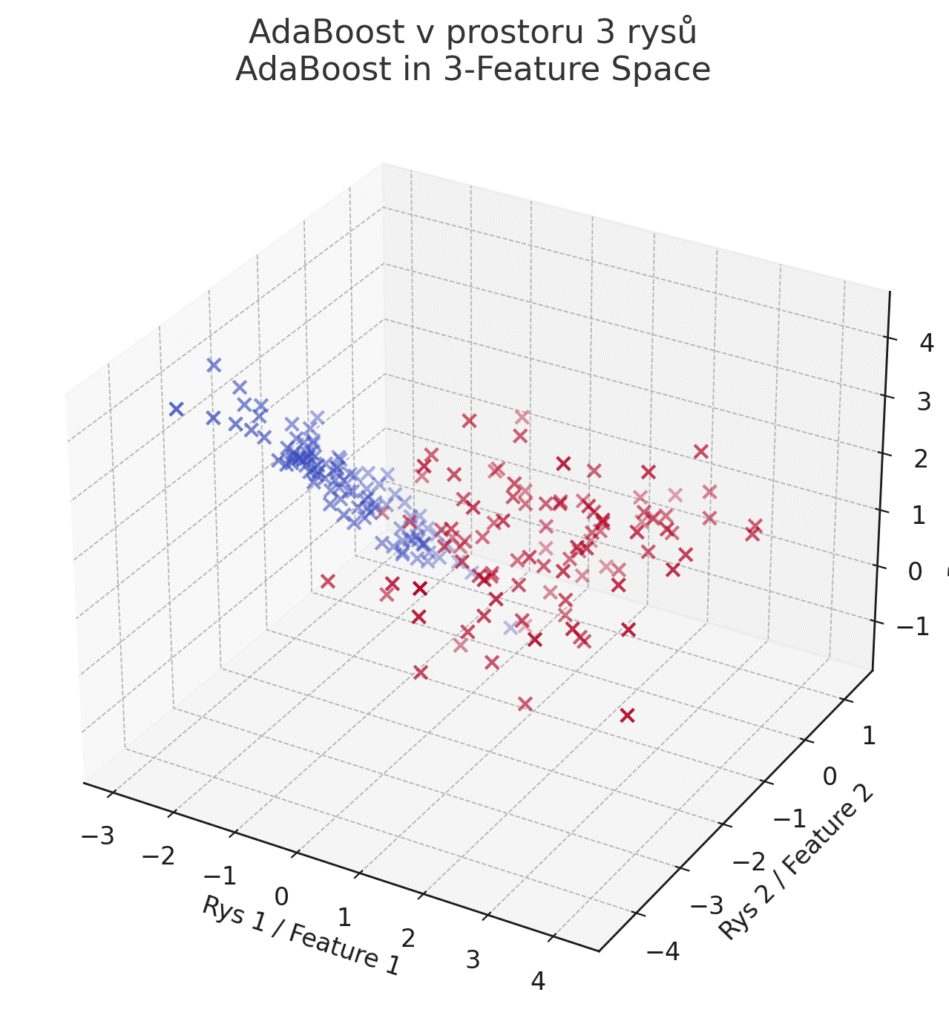
3D vizualizace Klasifikace pomocí AdaBoost na datech se třemi vstupními rysy. Jde o 3D rozmístění predikovaných tříd, nikoli rozhodovací hranici (tu ve 3D už zobrazit přímo nelze bez komplikovaných mřížkových řezů). Každý bod je zobrazen v prostoru podle hodnot tří rysů. Barva znázorňuje výstup predikce (dvě třídy).
Gradientní boosting (XGBoost, LightGBM aj.)
Gradientní boosting je vylepšení myšlenky AdaBoostu – místo abychom chyby penalizovali váhami dat, řeší se boosting jako sekvenční optimalizace gradientního sestupu v prostoru funkcí. Bez zacházení do detailů to znamená, že nové slabé modely jsou trénovány tak, aby aproximovaly gradienty chyb předchozího ensemble (tj. učí se přímo z reziduálních chyb). Typicky se také používají rozhodovací stromy jako slabé modely, ale mohou být i hlubší než pařezy.
Výsledkem je velmi výkonný ensemble model známý jako Gradient Boosted Trees (GBDT). Prosadily se specializované knihovny implementující gradientní boosting extrémně efektivně – zejména XGBoost a LightGBM (dalším je např. CatBoost). Tyto algoritmy dominují mnoha soutěžím a aplikacím, zejména na strukturovaných tabulkových datech, kde často překonávají i neuronové sítě v poměru výkon/výpočet.
XGBoost (Extreme Gradient Boosting)
Jde o populární open-source knihovnu, která přinesla řadu optimalizací pro boosting. XGBoost implementuje regularizaci L1/L2 pro omezení přeučení, využívá paralelní výpočet (trénuje více větví stromu souběžně) a efektivní způsob prořezávání stromů. Také umí zacházet s chybějícími hodnotami elegantně (sám rozhodne, na kterou větev je poslat).
XGBoost proslul v komunitě datových soutěží – stal se go-to algoritmem na Kaggle, kde vyhrál mnoho soutěží Najdeme jej ale i v průmyslu, například ve finančních modelech (predikce rizika, detekce podvodů) nebo zdravotnictví, kde je potřeba vysoká přesnost predikcí. Díky své robustnosti je využíván i pro detekci anomálií.
LightGBM
Knihovna od Microsoftu, která zrychlila boosting pomocí tzv. histogramové metody učení. Místo procházení všech možných prahů kontinuálních proměnných (což je u stromů náročné) převádí LightGBM hodnoty rysů do adaptivních histogramů a pracuje s těmito biny. Tím výrazně zrychluje trénování a snižuje paměťové nároky, zvláště na velkých datech.
LightGBM také používá inovativní způsob růstu stromu – tzv. leaf-wise (rozšiřuje nejprve list s největším zlepšením), což může vést k hlubším specializovaným stromům, ale s parametrem na omezení přerůstání. Výhodou LightGBM je i nativní podpora kategoriálních proměnných (nemusí se one-hot kódovat). Využívá se v aplikacích, kde jsou velké objemy dat a požadavek na rychlost – např. real-time predikce v online systémech (reklamní aukce, doporučování) LightGBM dokáže rychle zpracovat i obrovské datasety, kde by jiné algoritmy byly pomalé nebo by se nevešly do paměti.
| Výhody | Nevýhody |
| Moderní boostingové algoritmy dosahují špičkové přesnosti na mnoha úlohách. Kombinují přednosti stromů (nelineární modelování, práce s různými typy dat) s ensemble silou. Oproti náhodnému lesu často lépe optimalizují chybu – každitá nový strom cíleně snižuje reziduální chybu, což vede k vyšší přesnosti s méně stromy. XGBoost a LightGBM jsou navíc velmi efektivní implementace – využívají paralelismus, optimalizované datové struktury a triky pro rychlost. Podporují také spoustu nastavení pro regularizaci (např. maximální hloubka stromů, učení s podvzorkováním dat či rysů, penalizace složitosti stromů) pro kontrolu přeučení. Další výhodou je robustnost – umí si poradit s chybějícími hodnotami a často nevyžadují rozsáhlou předběžnou úpravu dat (např. normalizaci). | Cena za výkon je vyšší výpočetní náročnost při trénování – boosting je sekvenční, každý nový strom čeká na výsledky předchozích, což omezuje paralelizaci v porovnání s náhodným lesem. Trénování může být pomalejší, obzvlášť pokud je požadováno mnoho iterací (stovky až tisíce stromů). Paměťová náročnost může narůst u velkých dat (XGBoost je znám, že při defaultním nastavení může spotřebovat hodně paměti, LightGBM je v tomto úspornější). Interpretovatelnost je opět nízká – i když můžeme zkoumat důležitost rysů (feature importance) a dílčí stromy, celkově je model složen z mnoha komponent a jeho rozhodování není transparentní. Pro nasazení je predikce mírně pomalejší než u jednoho stromu, ale pokud je počet stromů rozumný (stovky), stále je to zvládnutelné i v reálném čase. Obecně platí, že gradientní boosting může přeučit, pokud se například použije příliš mnoho stromů nebo příliš vysoká hloubka bez dostatečné regularizace. Proto je důležité pečlivě ladit hyperparametry. |
Typické použití gradientního boostingu
Gradient boosting (hlavně XGBoost, LightGBM, CatBoost) je často klíčovou součástí vítězných řešení v soutěžích machine learning pro tabulková data – např. predikce cen nemovitostí, Klasifikace zákazníků, detekce podvodů. V oblasti FinTech a AdTech se boosting používá pro predikci rizik, hodnocení klientů, cílení reklamy, kde je spousta dat a mírně nelineárních vztahů – boosting zde exceluje kombinací přesnosti a rychlosti nasazení.
LightGBM nachází uplatnění tam, kde jsou miliardy záznamů (big data) – např. logy z webu, telemetrie – a je potřeba model, který se s takovým objemem dokáže vypořádat rozumně rychle.
Boosting modely lze využít i jako součást stacking v kombinaci s dalšími modely, kde výstupy z těchto více modelů (např. neuronové sítě, SVM, apod.) slouží jako vstupy pro metamodel – často jím bývá právě XGBoost pro finální rozhodnutí.
| Metoda | Zdroj diverzity | Způsob kombinace | Riziko přeučení | Paralelizace |
| Bagging (Random Forest) | Bootstrap vzorky + náhodné rysy | Průměr/hlasování | Nízké | Vysoká |
| Boosting (AdaBoost, XGBoost) | Sekvenční učení z chyb | Vážené hlasování | Střední-vysoké | Omezená |
| Stacking | Různé algoritmy | Metamodel | Nízké | Vysoká (level 0) |
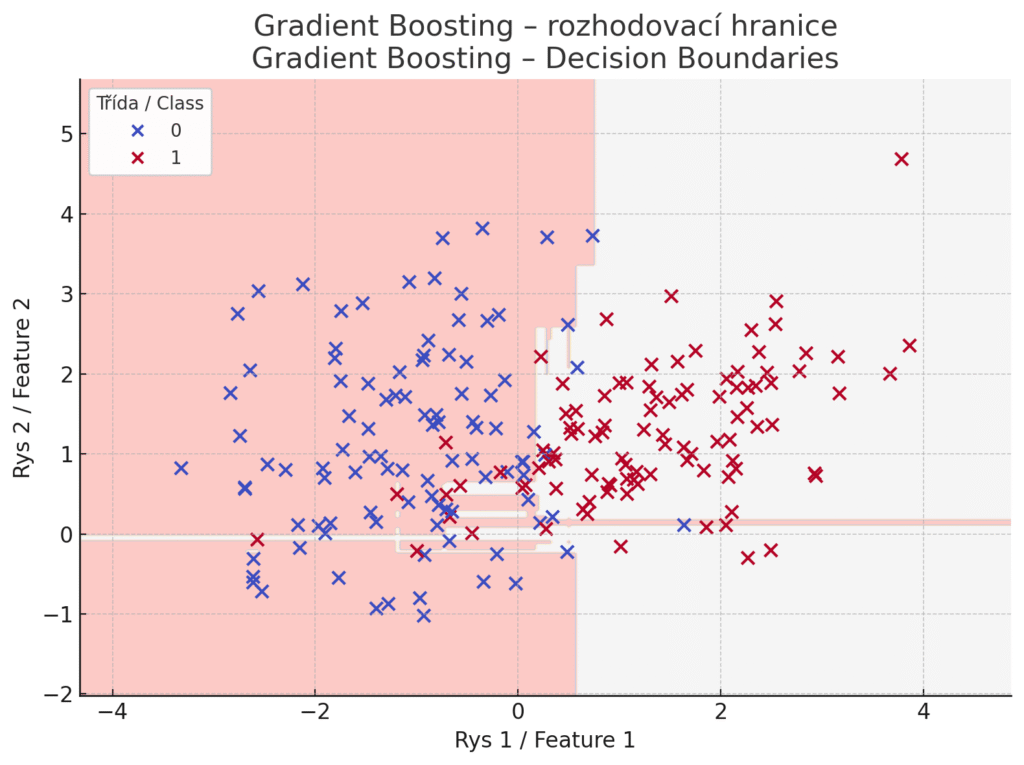
Fungování Gradient Boosting Classifieru – barevné oblasti zobrazují rozhodovací hranice, které vznikají jako výsledek sekvenčního trénování stromů – každý další model se snaží zlepšit předchozí tím, že se učí z jeho chyb. Na rozdíl od AdaBoostu se chyby neřeší váhami vzorů, ale jako gradienty ztrátové funkce, které nové modely aproximují. Model se skládá z více stromů, které nejsou nezávislé, ale navazují na sebe.
Porovnání algoritmů
Nyní, když jsme si prošli jednotlivé algoritmy, podíváme se na jejich vzájemné srovnání z hlediska přesnosti, výpočetní náročnosti, interpretovatelnosti a vhodné velikosti dat.
| Algoritmus | Kvalita/Validace | Výpočetní náročnost (trénink / inference) | Interpretovatelnost | Velikost dat |
|---|---|---|---|---|
| Logistická Regrese | Střední (lineární model) | Velmi nízká / velmi nízká | Vysoká (váhy snadno vysvětlitelné) | Malé i velké (škáluje dobře) |
| Lineární Regrese | Střední (lineární model) | Velmi nízká / velmi nízká | Vysoká (koeficienty snadno interpretovatelné) | Malé i velké (škáluje dobře) |
| Rozhodovací strom | Střední (jednodušší model) | Nízká / nízká (rychlé rozhodování) | Vysoká (snadno čitelná pravidla) | Malé až střední (u velkých lépe ensemble) |
| Náhodný les | Vysoká (ensemble stromů) | Střední / střední (mnoho stromů) | Nižší (mnoho stromů komplikuje) | Střední až velké (škáluje s paralelizací) |
| KNN | Střední (záleží na datech) | Zanedbatelná / Rostoucí s velikostí dat | Nízká (těžko interpretovat, příklady) | Malé (velká data = pomalé dotazy) |
| SVM | Vysoká (s vhodným jádrem) | Vysoká / Nízká-střední (náročné učení, rychlá predikce při malém počtu support vectors | Nízká (černá skříňka pro nelineární) | Malé až střední (velká data = pomalé učení) |
| Naivní Bayes | Nižší až střední (jednoduchý) | Velmi nízká / velmi nízká | Střední (pravděp. hodnoty částečně srozumitelné) | Malé i velké (rychlý pro jakékoli objemy) |
| Umělé sítě (ANN) | Vysoká až velmi vysoká (závisí na architektuře, datech a ladění) | Velmi vysoká / Střední (náročný trénink, inference dle velikosti) | Velmi nízká (neinterpretovatelná) | Spíše velké (potřebují hodně dat) |
| K-means | Silhouette, Davies-Bouldin index | Střední / nízká (iterativní učení, rychlá Klasifikace) | Nízká (shluky je třeba interpretovat) | Střední až velké (škáluje lineárně) |
| SOM | Topological error, kvantizační chyba | Střední / střední (O(n × epochs), rychlá Klasifikace) | Nízká (oblasti mapy obtížně interpretovatelné) | Střední (vhodné pro vizualizaci středních dat) |
| PCA | Explained variance ratio | Střední (náročné pro mnoho rysů) / nízká | Nízká (komponenty obtížně vysvětlitelné) | Střední (velmi velká data vyžadují přibl. metody) |
| AdaBoost | Vysoká (zlepšuje slabé mod.) | Střední / střední (sekvenční ensemble) | Nízká (kombinace mnoha slabých modelů) | Malé až střední (citlivý na šum ve velkých) |
| Gradientní boosting | Velmi vysoká (špičkový výkon) | Vysoká / střední (mnoho iterací) | Nízká (black-box ensemble) | Střední až velké (optimalizován pro velká data) |
| └─ XGBoost | Velmi vysoká | Střední-vysoká / střední (efektivní C++ impl.) | Nízká (je třeba využít např. důležitost rysů) | Střední až velké (Kaggle standard) |
| └─ LightGBM | Velmi vysoká | Nízká-střední / střední (vysoce optimalizováno) | Nízká (podobné jako XGBoost) | Velké (škáluje na masivní data) |
(Pozn.: „Kvalita/Validace“ u supervised metod označuje obecnou schopnost modelu dosahovat nízké chyby – skutečná přesnost závisí na povaze dat. U nesupervizovaných metod se uvádějí specifické metriky pro hodnocení kvality shlukování nebo dimenzionality.)
Z tabulky je vidět několik trendů. Jednoduché modely jako logistická regrese nebo rozhodovací strom jsou rychlé a snadno pochopitelné, ale nemusí dosahovat nejvyšší přesnosti na složitých problémech. Komplexnější modely – ensemble stromy (náhodný les, boosting) a hluboké neuronové sítě – obvykle nabízejí vyšší přesnost, zvláště pro velké a komplexní datasety, avšak za cenu vyšší výpočetní náročnosti a ztráty interpretovatelnosti. Například hluboká neuronová síť nebo XGBoost mohou odhalit velmi komplexní vztahy ve velkém objemu dat a dosáhnout špičkové výkonnosti, ale výsledný model je pro člověka neprůhledný a vyžaduje dostatek dat i výpočetního výkonu k natrénování. Naopak modely jako rozhodovací stromy či logistická regrese jsou vhodné, pokud potřebujeme vysvětlitelný model a máme spíše menší či střední dataset s jednodušší strukturou.
Dalším důležitým aspektem je výpočetní náročnost trénování vs. nasazení. U většiny algoritmů je nejnáročnější fáze trénování (učení se z dat), zatímco predikce (inference) bývá poměrně rychlá. Například SVM může trénovat dlouho, ale jakmile se najde rozhodovací hranice, Klasifikace nových bodů je otázkou výpočtu skalárních součinů se support vectors – při malém počtu support vectors je to rychlé, ale při tisících support vectors může být inference pomalejší. Podobně neuronovou síť je třeba iterativně učit na mnoho epoch, avšak výsledný model pak dokáže predikovat v milisekundách až sekundách (pokud má dostatečný hardware). Výjimkou je KNN, kde trénování je triviální (uložení dat), ale nasazení vyžaduje porovnání s celou trénovací množinou, takže s rostoucími daty se predikce zpomaluje. Proto se KNN hodí jen pro menší objemy dat nebo je nutné použít optimalizace.
Interpretovatelnost vs. přesnost často stojí proti sobě – jednodušší modely (lineární, stromy) jsou více interpretable, zatímco modely s vysokou kapacitou (ensemble, hluboké sítě) poskytují vyšší přesnost za cenu „černé skříňky“. Tento trade-off je známý a v praxi se řeší i pomocí technik vysvětlitelné AI (např. odvození důležitosti rysů, aproximace složitého modelu jednodušším apod.). Z pohledu velikosti dat lze říci, že pro malé datasety jsou vhodné spíše jednodušší modely – komplexní model by se je mohl naučit nazpaměť (přeučit) bez schopnosti generalizace. Naopak pro velmi velké datasety je často nezbytné použít modely, které dokážou škálovat a využít potenciál dat (např. LightGBM pro tabulková data, nebo hluboké sítě pro obrazové či textové). Některé algoritmy (např. SVM s nelineárním jádrem, KNN) nejsou praktické pro miliony vzorků kvůli výpočetnímu zatížení. V takovém případě se volí buď jednodušší verze (lineární SVM, aproximované KNN), nebo úplně jiné metody.
Tak jaký algoritmus mám vlastně použít?
V oblasti strojového učení neexistuje jeden univerzálně nejlepší algoritmus – volba závisí na povaze úlohy, dostupných datech a požadavcích.
Možná by vám mohla pomoci následující vodítka…
Když mám malá data a snadnou interpretaci
Začněte s logistickou regresí nebo rozhodovacím stromem. Tyto modely poskytnou rychlou odezvu a jejich výsledky lze snadno vysvětlit v obchodních souvislostech. Například u jednoduché Klasifikace (ano/ne) s pár stovkami záznamů bude logistická Regrese často dostačující a nabídne jasný pohled na vliv jednotlivých vstupů. Rozhodovací strom zase pomůže odhalit klíčová rozhodovací pravidla.
Když záleží na každém procentu přesnosti na strukturovaných datech
Vyzkoušejte ensemble metody. Náhodný les je dobrý výchozí bod – často poskytne solidní výsledky bez velkého ladění. Pokud však potřebujete maximum výkonu, sáhněte po XGBoost nebo LightGBM. Tyto gradientní boosting modely typicky dosahují nejvyšší přesnosti na tabulkových datech. Pamatujte však na riziko přeučení – hlídejte parametry jako hloubka stromů, počet iterací a používejte křížovou validaci pro ověření výkonu.
Mám hodně dat a málo času
Pokud máte miliony řádků a chcete rychle trénovat model, LightGBM může být vhodnější než náhodný les či klasický SVM – LightGBM je navržen pro škálování na velká data a může zvládnout i velmi objemné úlohy. Také lineární modely (lineární Regrese, logistická Regrese nebo lineární SVM) dokážou zpracovat velké množství dat rychle díky jednoduché funkční formě. Neuronové sítě mohou též zpracovat velké objemy, ale trénovací čas a potřeba ladění jsou faktory, se kterými je nutno počítat.
Na opravdu komplexní data (obraz, text, zvuk) s mnoha vlastnostmi
Zde často kralují hluboké neuronové sítě. Pokud řešíte úlohu rozpoznávání obrazu nebo přirozeného jazyka, moderní architektury neuronových sítí (CNN, RNN, Transformers) zpravidla nabídnou nejlepší výsledky. Je však třeba dostatek trénovacích dat a výpočetních zdrojů. Pro rychlý start lze využít i předtrénované modely (transfer learning), aby nebylo nutné trénovat vše od nuly. U menších projektů lze jako baseline vyzkoušet i SVM nebo jednodušší modely s ručně vytvořenými příznaky, ale obecně v těchto doménách hluboké učení vede.
Když nevím, co hledám
Jestliže nemáte trénovací cíle (labels), pak pro exploraci dat a odhalení struktur použijte shlukování nebo snížení dimenze. K-means je dobrým výchozím shlukovacím algoritmem, pokud tušíte, kolik skupin hledat. Pro vizualizaci či předzpracování dat se hodí PCA, případně pokročilejší metody, pokud linearita PCA nestačí. Tyto techniky vám mohou pomoci lépe porozumět datům, najít segmenty nebo připravit vstupy pro následné modelování.
Jak se na to všechno podívat?
Výběr algoritmu by měl být veden experimenty. Doporučený postup zkušených profesionálů je vyzkoušet nejprve jednodušší interpretovatelné modely pro získání základní představy o datech a nastavení referenčního výkonu (baseline). Následně lze zkoušet komplexnější algoritmy a ověřovat, zda přinášejí zlepšení výkonu.
Zároveň sledujte i další okolnosti a faktory, třeba pokud potřebujete model nasadit v reálném čase na zařízení s omezeným výkonem, příliš složitý model může být nepraktický. Naopak pro off-line analýzy může být delší trénování akceptovatelné.
Důležitá je i údržba a interpretace – v některých aplikacích (např. zdravotnictví nebo finance) může být jednodušší, vysvětlitelný model preferován před nepatrně přesnějším, ale „neprůhledným“ modelem kvůli důvěryhodnosti a požadavkům regulace.
Výběrem správného algoritmu tedy zvažujeme kompromisy mezi přesností, komplexitou a srozumitelností. S praxí a zkušenostmi získáte lepší odhad, který typ modelu se pro daný problém hodí. Tento článek vám poskytl základní přehled a srovnání, které může začínajícím datovým nadšencům pomoci udělat informované rozhodnutí při prvních projektech v oblasti strojového učení.
Moderní trendy v strojovém učení zahrnují AutoML pro automatické ladění hyperparametrů, explainable AI techniky (SHAP, LIME) pro lepší interpretovatelnost složitých modelů a stacking - pokročilou ensemble metodu, kde výstupy různých modelů slouží jako vstupy pro metamodel. V praxi se také důraz klade na etické aspekty a férovost modelů - například metriky jako Equal Opportunity nebo Demographic Parity, s nástroji jako Fairlearn v Pythonu - a jejich transparentnost, zejména v citlivých oblastech jako zdravotnictví nebo finance.Přehled základních algoritmů strojového učení přehledně v tabulce
| Algoritmus | Výhody | Nevýhody | Doplňující poznámky |
|---|---|---|---|
| Logistická Regrese | Méně náchylná k přeučení, rychlý trénink. Skvělá interpretace (odds ratio, P-hodnoty). | U vysoko-dimenzionálních dat se může přeučit, trpí multikolinearitou. Předpokládá lineární vztah mezi log-odds a vstupy. | Vhodná jako „baseline“ pro binární/multi-class klasifikaci, dobře funguje s regularizací (L1/L2). |
| Lineární Regrese | Extrémně rychlá, koeficienty snadno interpretovatelné. Regulace (Ridge/Lasso) snižuje přeučení. | Silné předpoklady (linearita, homoskedasticita, normalita residuí). Citlivá na odlehlé hodnoty a šum. | Vhodná pro odhad spojité veličiny u lineární závislosti; na nelinearitu je nutné rozšířit rysy/přidat polynomy. |
| Rozhodovací strom (Decision Tree) | Řeší nelineární problémy, zvládá numerické i kategorické rysy. Snadná vizualizace a vysvětlení. | Vysoké riziko přeučení; malá změna dat → jiný strom. Bias vůči atributům s mnoha úrovněmi. | Přeučení se tlumí prořezáváním, baggingem či Random Forest. |
| Náhodný les (Random Forest) | Vysoká přesnost díky ensemble, odolný vůči šumu. Odhaduje důležitost rysů, méně přeučení než jednotlivý strom. | Interpretovatelnost omezená (stovky stromů), vyšší výpočetní náročnost než jeden strom. | Oblíbený pro tabulková data, zabudovaná feature importance pro výběr rysů. |
| K-NN | „Lazy learner“ – žádná fáze učení, jednoduché. Použitelný pro klasifikaci i regresi. | Špatně škáluje na velké datasety, paměťově náročný. Citlivý na škálu rysů, šum a volbu K. | V praxi se kombinuje s indexovacím / aproximačním vyhledáváním (KD-tree, FAISS). |
| SVM (Support Vector Machine) | Výborné pro vysoko-dimenzionální data a malé vzorky. Kernelové triky → nelineární rozhodovací hranice. | Trénink je O(n²–n³), nevhodné pro miliony vzorků. Citlivé na volbu jádra, C a γ; obtížně interpretovatelné. | LinearSVM (+SGD) řeší škálování; nutné pečlivé standardizování rysů. |
| Naivní Bayes | Velmi krátký trénink, funguje i na malém množství dat. Oblíbený pro textovou klasifikaci (vysoká dimenze). | Silný (často porušený) předpoklad podmíněné nezávislosti rysů. Problém nulové frekvence (řeší Laplaceovo vyhlazení). | Překvapivě konkurenceschopný, pokud jsou rysy víceméně nezávislé. |
| ANN (Umělé neuronové sítě) | Umí modelovat složité nelineární vztahy. Dobrá generalizace, možnost paralelizace na GPU/TPU. | Dlouhý trénink a četné hyperparametry. „Black-box“ – nízká interpretovatelnost, nutné velké množství dat. | Moderní rámce (PyTorch, TensorFlow) usnadňují vývoj; explainability řeší SHAP, LIME apod. |
| K-means (shlukování) | Jednoduché, rychlé a škálovatelné. Zaručená konvergence do lokálního minima. | Citlivé na odlehlé body a počáteční centroidy. Volba K nebývá zřejmá (Elbow, Silhouette). | Předpokládá sférické clustery; pro jiné tvary lze zvolit DBSCAN či GMM. |
| SOM (Self-Organizing Maps) | Zachovává topologii, vynikající vizualizace komplexních dat, relativně rychlý trénink O(n × epochs). | Citlivost na volbu rozměru mřížky a počáteční váhy, obtížná interpretace oblastí mapy. | Výhradně explorační nástroj pro vizualizaci a segmentaci vysokodimenzionálních dat. |
| PCA (Analýza hlavních komponent) | Redukuje korelované rysy → nižší rozměr a méně přeučení. Zrychluje následné modely. | Komponenty jsou těžko interpretovatelné. Nevyhnutelná ztráta informace; vyžaduje standardizaci. | Často krok před klasifikací/regresí nebo vizualizací (2D/3D). |
| AdaBoost | Ensemblový přístup zvyšuje přesnost a tlumí přeučení. Jednoduchá implementace (slabé učitele + váhy). | Vysoce citlivý na šum a odlehlé hodnoty. Sekvenční charakter → pomalejší než bagging. | Nejčastějším slabým učitelem je stump (1-úrovňový strom). |
| Gradientní boosting (XGBoost, LightGBM) | Špičková přesnost na tabulkových datech, efektivní implementace s paralelizací a regularizací. | Vyšší výpočetní náročnost, mnoho hyperparametrů k ladění, black-box model. | Dominuje Kaggle soutěže, často go-to volba pro strukturovaná data v průmyslu. |
Licence článku: Tento článek je licencován pod Creative Commons. Můžete jej volně sdílet a upravovat, pokud uvedete autora a odkaz na tento text.
